Iwahara et al. first reported the proton conduction in the perovskite structures such as SrZrO₃ and SrCeO₃ in 1980, and many following studies have been carried out on the phenomena taking place in the interior of oxides.^1-2) Among many proton-conductors, the acceptor-doped barium zirconate (BaZrO₃, BZO) has been intensively studied as an electrolyte of protonic ceramic fuel cell (PCFC) because of its high proton conductivity through the grain interior and sound chemical stability.^3-12) However, the low proton conductivity across the grain boundary compared to that of grain interior has been recognized as a critical issue.^3-13)

The low proton conductivity of BZO grain boundary has been often interpreted with the space charge layer (SCL) model, in which the positively charged protons accumulate in grain boundary.^3-13) Another model, the structural disorder (SD) model, has attributed the cause of low proton conductivity to the increased energy barrier for proton transport by the disordered grain boundary.³⁾ Recently, Yang et al. proposed an hybrid model of SCL and SD models, and investigated proton conductivity of a ∑3 BZO (111)[11̄0] grain boundary by using density functional theory (DFT).¹³⁾

Studies on SCL formation focused mainly on the stoichiometric BZO grain boundary, and rarely on the nonstoichiometric ones.^9-13) Helgee et al., for example, investigated SCL formation for three stoichiometric BZO cases using DFT; ∑3 (110)[11̄0], ∑3 (112)][11̄0], and ∑3 (210)[001] BZO grain boundaries.⁹⁾ They confirmed that Schottky barrier heights are in the same range of 0.6 V at 600K although the grain boundary structures are different.⁹⁾ Polfus et al. also investigated the SCL formation on a stoichiometric ∑3 BZO (111)[11̄0] grain boundary using DFT, and reported the height of 0.51 V at 573K.¹⁰⁾ These two studies indicate that Schottky barrier heights are not affected much by the orientation of the grain boundaries.

Only limited studies are available for the nonstoichiometric grain boundary structures such as SrTiO₃ and BaTiO₃.^14-15) Kim et al. studied SrTiO₃ structure by STEM (scanning transmission electron microscope), and found that the grain boundary is nonstoichiometric.¹⁴⁾ Choi et al. measured the Ba/Ti ratio of BaTiO₃ by HREM (high resolution electron microscope), and mentioned that the grain boundary compared to the bulk grain has more Ti atoms.¹⁵⁾ Recently, Kim et al. evaluated stability of the nonstoichiometric ∑3 BZO (210)[001] grain boundary in terms of oxygen partial pressure and oxygen chemical potential using DFT, and reported that the nonstoichiometric grain boundary is more stable compared to the stoichiometric one.¹⁶⁾

Thus, proton conductivity evaluation at the operation temperature of PCFC with a stable nonstoichiometric BZO grain boundary is important. We design a grain boundary of nonstoichiometric ∑3 BZO (210)[001] for this study by following the SCL model, and calculate the Schottky barrier height and estimate the concentration of proton. We calculate the energy barrier of proton along the minimum transport path, and estimate the proton mobility based on it. We also calculate proton conductivity with proton concentration and its mobility at the grain boundary of the system, and compare it with other reported experimental and theoretical results.

All calculations in this study were carried out within the framework of the DFT using the Vienna Ab-initio Simulation Package (VASP).^17-20) Electron wave function was described by the Blöchl’s projector augmented wave (PAW) method formulated by Kresse and Joubert^21-22) with the exchange-correlation energy of Perdew-Burke-Ernzerhof (PBE) parameterization within the generalized gradient approximation (GGA).^23-24) We considered the strong correlation effect for Zr atom by using U_eff (U - J) of 3 eV proposed by Vladan et al. in their study on the formation energy correction for oxides.²⁵⁾

We used a cutoff energy of 500 eV, and generated a kpoint grid of 8×8×8 by the Monkhorst-Pack method.²⁶⁾ The orbital occupation by electron at the Fermi level was smeared by the Gaussian method with a smearing factor of 0.05 eV. Electronic and ionic minimizations were carried out until total energy convergence of less than 10⁻⁴ and 10⁻³ eV, respectively. The geometric structure was optimized until each atom’s residual force falls below 0.02 eV/Å. We also analyzed the electronic structure of grain boundary using Bader charge calculation.²⁷⁾ The energy barrier for proton transport was determined by using the climbing image nudged elastic band (CINEB) method.²⁸⁾ All illustrations were drawn by using the Visualization for Electronic and Structural Analysis (VESTA) program.²⁹⁾

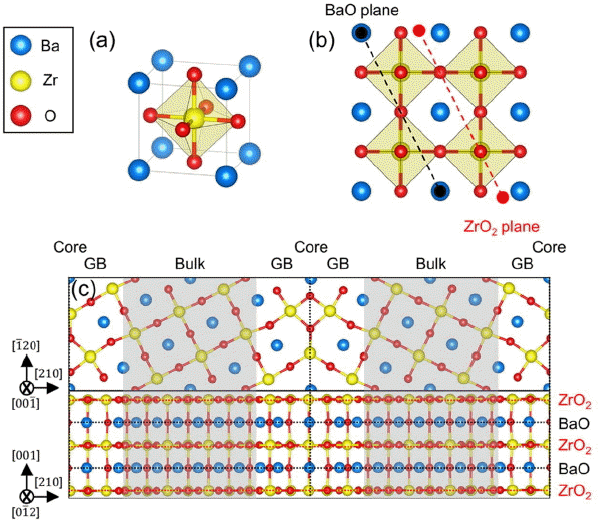
Figure 1(a) shows the perspective view of the optimized BZO unit cell with a lattice constant of 0.428 nm, in agreement with the experimental value of 0.415 nm.³⁰⁾ Fig. 1(b) is the (210) surface of a 2 × 2 × 2 BaZrO₃ super cell formed with BaO and ZrO₂ planes. Note that Kim et al. formed stoicheometric and nonstoicheometric ∑3 BaZrO₃ (210)[001] grain boundaries using the same BaO and ZrO₂ planes, and computationally evaluated its stability in terms of temperature, pressure, and chemical potential.¹⁶⁾ Fig. 1(c) represents the nonstoicheometric ∑3 BaZrO₃ (210)[001] grain boundary, which is found to be the most stable.

We introduced the SCL model in order to calculate the electrostatic potential, and concentration (c_D, D =H or V) of proton (H) and oxygen vacancy (V) formed in grain boundary. ^6-11,31) Dopant concentration of 10% was assumed to be uniformly distributed in the grain boundary structure by following the Mott-Schottky approximation. The partial pressure of water and dielectric constant were set as 0.025 atm and 75, respectively.^3,13) The hydration enthalpy and entropy in grain interior were set at −0.79 eV and −0.89 meV/K, respectively.^3,13) Mobility of H (μ_H) was calculated by the following equation.

Here, D₀ is the maximum diffusion coefficient, q_H is the charge of H, E_m is the transport energy barrier of H, k_B is the Boltzmann’s constant, and T is temperature. Conductivity of H (σ_H) is calculated by the following equation using the concentration and mobility of H (c_H and μ_H).

Readers may refer to the paper by Yang et al. for details of SCL model and σ_H.¹³⁾

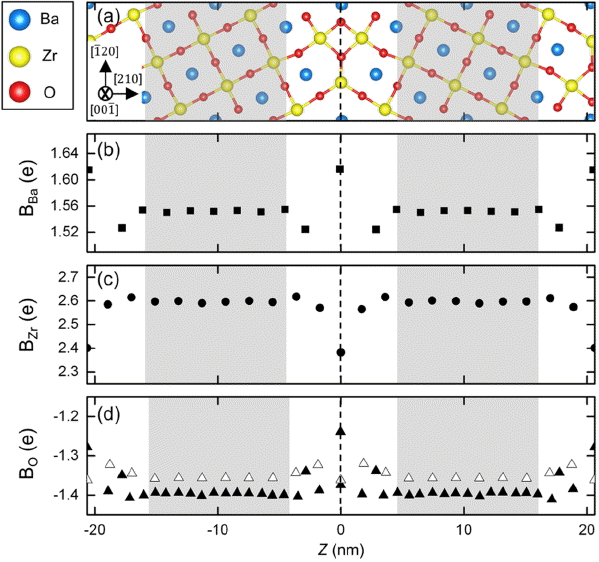
Figure 2 shows Bader (B_i, i = Ba, Zr, O) charges of (a) Ba, (b) Zr, and (c) O atom in the nonstoichiometric ∑3 BZO (210)[001] grain boundary along the distance from the grain boundary core (z = 0). The black square, black circle, black triangle, and empty triangle indicate the B_Ba, B_Zr, B_O in the ZrO₂ layer, and B_O in the BaO layer, respectively. The vertical dashed line represents the grain boundary core (z = 0), and white and grey regions are grain boundary and grain interior, respectively. In the grain boundary core, B_Ba became more positive, B_O less negative, and B_Zr less positive compared with their bulk values.

Since O atoms coordinate with two and three Zr atoms in grain interior and grain boundary, respectively, the O atoms in grain boundary are positively charged compared to the other case. Charges of B_Ba and B_Zr in grain interior converged to 1.55 and 2.60 e, respectively. B_O in the BaO and ZrO₂ layers converged to 1.35 and 1.40 e, respectively. This may attribute to the difference in atomic arrangement in the BaO and ZrO₂ layers. We also confirmed that B_Ba and B_Zr are symmetric along the base line of Z = 0, but B_O is slightly asymmetric.

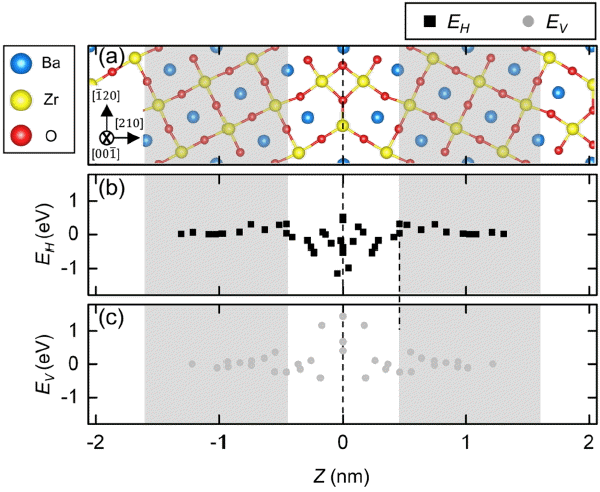
Figure 3 shows the ∑3 BZO (210)[001] grain boundary, and changes of H and V formation energy (E_D, D = H or V) along the distance from Z = 0. We calculated E_D by the following equation.

Here, EDGB and EDB are energies when H or V is in the grain boundary or in the grain interior, respectively. We determined EDB as the reference defect energy when the charged defect is located far from the grain boundary core. In the figure, the black square and grey circle are E_H and E_V, respectively, and the vertical dashed line indicates the grain boundary core (Z = 0). Note the presence of O sites with higher E_H and E_V in the core compared to the grain interior.

O atoms coordinated with three Zr atoms have positive charges compared to O atoms in the grain interior, which leads to the formation of H or V and likely makes the grain boundary rather unstable. E_H in the grain boundary core is in the range of −1.16 ~ 0.58 eV, which is indicative of a stable segregation of H to the grain boundary. Note also that E_H in the grain boundary region is asymmetric, which may be due to the changed B_O from structural variation. V also could stably segregate to the grain boundary region, and its E_V is in the range of −0.6 ~ 0.6 eV.

Yang et al. considered the multi-H (multi-proton) effect to calculate the segregation energy (E_H,seg) more precisely. They averaged E_H for the excessively-segregated H adjacent to the grain boundary core.¹³⁾ Under the hydration condition, however, there is no need to consider the multi-V effect, since its concentration is very low in the core.^9-13,16) We further clarified that H can segregate easier to the grain boundary compared to V, since E_H,seg (−0.70 eV) is lower than E_V,seg (−0.54 eV).

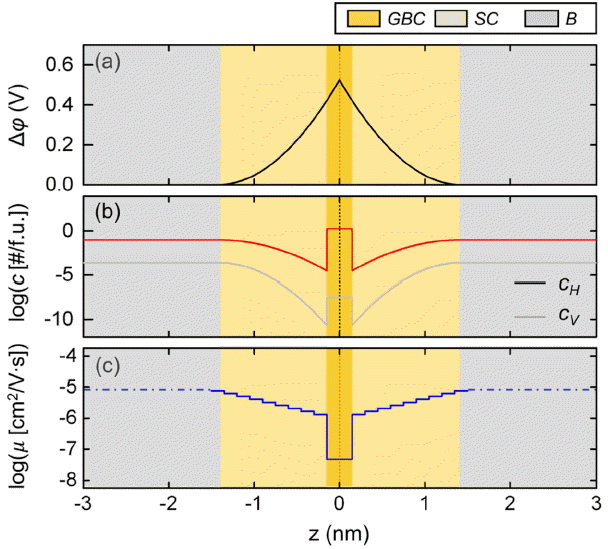
Figure 4(a) shows the change of the electrostatic potential, ϕ(z), as a function of z at 600K. Dark yellow, light yellow, and grey zones indicate GBC, SCL, and B, respectively. As a consequence of the segregated H to the grain boundary region, a Schottky barrier height (Δϕ(0)) as calculated by the following equation appeared in the grain boundary core.

Here, ϕ(0) and ϕ(∞) are electrostatic potentials in the grain boundary core and far away from it, respectively. We obtained Δϕ(0) of 0.52 V and SCL thickness (λ) of 1.46 nm at 600K. We found that these are very close to the values of 0.51 V and 1.41 nm, respectively, reported by Yang et al.¹³⁾

Figure 4(b) shows change of c_H and c_V (represented by red and grey lines, respectively) as a function of z at 600K. c_H is high at the GBC, but c_V with the same positive charge is very low. In the SCL region right next to the GBC of 0.3 nm, concentrations of c_H and c_V become very low, and increase gradually toward the B region.

Figure 4(c) shows change of H mobility ( μHi, i = GBC, SC, B) as a function of z at 600K. The blue line stands for μHGBC and μHSC, and the blue dash-dotted line stands for μHB. Referring the 12.5% Y-doped case,³²⁾ we used EmB of 0.45 eV, and assumed that EmSC and EmB are the same. We referred the details of EmB and D₀ to the work by Yang et al.¹³⁾ For EmGBC, we used 0.61 eV which is the value when a proton passes through the minimum energy path across the grain boundary structure. H mobility across the grain boundary core, μHGBC, was about 10⁻⁷ cm²/V·s at 600 K, which is lower than μHBof 10⁻⁵ cm²/V·s.

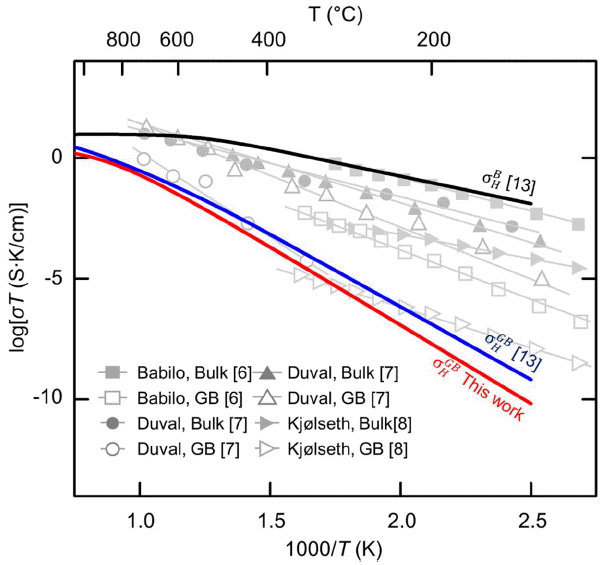
Figure 5 shows change of proton conductivity as σT against reciprocal temperature (1000/T) based on the calculated c_H and by using the SCL and SD models. The black, blue, and red lines represent σHB, σHGB of the stoichiometric ∑3 BZO(111)[11̄0], and σHGB of nonstoichiometric one, respectively.¹³⁾ The grey filled and open symbols indicate the experimentally measured σHB and σHGB from the literature, respectively.^6-8) Note that the calculated σHB shows the same trend with those by experiments, and that increase in temperature changes the slope of conductivity. This change in slope can attribute to the reduced c_H in bulk grain due to dehydration with increasing temperature.¹³⁾ σHGB for both stoichiometric and nonstoichiometric grain boundaries are lower than that for grain interior, and display the same trend with experimental σHGB. We concluded that stoichiometry has only minor effects on σHGB, although of the nonstoichiometric grain boundary shows slightly lower value.

We evaluate proton conduction for the nonstoichiometric ∑3 BaZrO₃ (210)[001] tilt grain boundary using DFT. We introduce H and V into the grain boundary to calculate c_H and c_V using SCL model, and observe positional changes of energy. We confirm that both H and V prefer to segregate to the grain boundary core to be more stable with E_H,seg and E_V,seg of −0.70 and −0.54 eV, respectively. The barrier energy for H crossing the grain boundary core is 0.61 eV by the SD model, which leads to calculation of μ_H. We conclude that stoichiometry has only minor effects on σHGB, although σHGB of the nonstoichiometric grain boundary shows slightly lower value.