1. Introduction
Piezoelectric ceramic materials are widely used in various fields as sensors, actuators, and memory devices. The researches on the development and applications of piezoelectric elements and systems continue to be actively carried out. Nonetheless, unpredicted and unnecessary domain switching and changes in the internal structure of the piezoelectric elements and systems have frequently been reported to occur during usage, due to an excessive concentration of electric field or stress, and a resulting rapid rise in temperature. Changes in the microscopic internal structure caused by such switching can lead to changes in the macroscopic properties of the piezoelectric material, and unpredictable nonlinear behavior. This can degrade the level of performance intended in the initial design.
Recently, studies were conducted to develop a model for predicting ferroelectric ceramic nonlinear behavior.1,2) However, most of the research was limited to modeling the behavior at constant room temperature, so there is still a need for expanded research on the behavior at high temperatures. Prior to developing a constitutive model, experimental data on changes in the behavior of remnant state variables and material property changes caused by changing temperatures, need to be acquired and analyzed.
Previous research on the modeling and behavior changes due to temperature variations include the following studies. Grunbichler et al.3) used a developed constitutive model for finite element analysis to understand the nonlinear behavior of piezoelectric materials caused by the stress, electric field, and temperature changes in a multistack piezoelectric actuator. Kungl et al.4) experimentally investigated the effect of temperature on poling strain when an electric field was applied to the piezoelectric material, and they also studied the temperature dependence of the remnant strain. Rauls et al.5) measured the hysteresis curves of PLZT ferroelectric materials, and Senousy et al.6) focused on the effect of the heat generated by the multistack piezoelectric actuator on the changes in the piezoelectric material properties, and performed a numerical analysis for the behavior of piezoelectric materias at high temperature, assuming a 2 stage 90-degree domain switching. Ji and Kim7) measured the hysteresis curve due to the electric field under various electric field loading rates and temperatures, and the measured data were used to predict the strain behavior. Kim and Kim8) measured the changes in remnant polarization and transverse remnant strain during temperature increase after an electric field was applied to a PZT wafer at room temperature. Ji and Kim9) measured the longitudinal and transverse strains of a rectangular PZT ceramic during temperature increase after electric field-induced switching at room temperature and measured the thermal expansion and pyroelectric coefficients. Also, Ji and Kim10) applied compressive stress at room temperature followed by temperature increase and obtained the changes in the pyroelectric and thermal expansion coefficients. Weber et al.11) measured and analyzed the nonlinear behavior of ferroelectric materials caused by compressive stress at high temperatures.
In this study, to measure the remnant polarization and remnant strains, an electric field was applied to a poled ferroelectric PZT specimen at room temperature in a direction opposite to the polarization, while increasing the temperature after switching and removing the electric field. Using the method reported by Ji and Kim,12) an empirical formula for the variations in polarization and strains was derived utilizing the measured data. The calculation values obtained through the derived empirical formula were compared with the experimental values and it was found that the switching process due to the electric field at different temperatures was equivalent from the perspective of macroscopic state variables.
2. Experimental Procedure
A cube PZT specimen with 10 mm sides was used in the experiment. Its density was 7400 kg·m−3 and the specimen was manufactured by a company in the UK (PZT5H1, Morgan Technical Ceramics, UK). The specimen was originally poled in the negative x3 direction(the thickness direction) and switching occurred when the electric field was loaded in the positive x3 direction at the reference temperature of 20°C. A change in the polarization density occurred when an electric field of 2 MVm−1 sinusoidal wave was 0.52 Cm−2 so the range of the reference remnant polarization density
P 3 R 0
In this study, electric fields of varying magnitude were applied a total of 14 times so that the magnitudes of reference remnant polarization were distributed at 0.04 Cm−2 intervals. The magnitudes of the applied electric field were 0, 0.520, 0.610, 0.649, 0.655, 0.660, 0.665, 0.671, 0.677, 0.684, 0.692, 0.726, and 0.880 MVm−1 and the derived reference remnant polarizations
P 3 R 0
In particular, after reaching
P 3 R 0
While the temperature increased, the remnant polarization
P 3 R
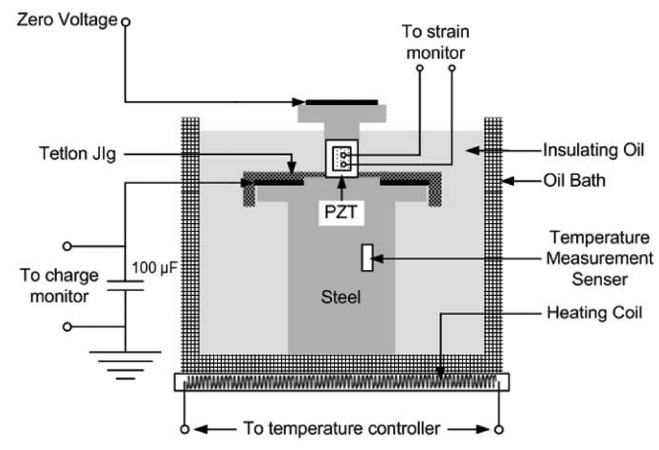
The polarization density was measured indirectly using the Sawyer-Tower circuit, and a Keithley 6514 was used to measure the voltage across the capacitor connected serially with the specimen. Changes in the thermal power were measured using strain gauges (WA-03-062TT-350, VISHAY, Germany) attached to the side of the specimens, which could be used in the temperature range from −75°C to 205°C.
The specimen temperature was controlled by placing it in a container (2408 PID controller, EUROTHERM, UK) shown in Fig. 1 with insulating oil (MICTRANS Class1-No2, MICHANG OIL IND. CO., Pusan, Korea) and heating the coil underneath the container. A Teflon jig with a square hole in the center was used as an insulating material between the lower portion of the specimen with high voltage and the grounded top part of the specimen.
All data were collected at 100 Hz through a DAQ unit (PCI 6221, National Instruments, TX, USA) and processed using the LabView program. The specifications of the specimen provided by the manufacturer were as follows. The specimen has a Curie temperature of 200°C, coupling factor of kp = 0.60, piezoelectric coefficients of d31 = −250 × 10−12 mV−1 and d33 = 620 × 10−12 mV−1, and elastic compliance coefficient of s33 = 21.9 × 10−12 m2N−1 and s11 = 17.7 × 10−12 m2N−1. Here, the subscript 3 refers to the polarization direction of the specimen and subscript 1 refers to the direction transverse to the polarization.
3. Result and Discussion
3.1. Changes in Remnant Polarization and Pyroelectric Coefficient During Temperature Increase
Electric fields of various magnitudes were applied to a PZT specimen, which had been poled in the specimen thickness direction. The electric fields were applied in the direction opposite to the polarization at the reference temperature of 20°C. Switching occurred due to the application of the electric field. After reaching a specific reference remnant polarization density, the electric field was removed and the temperature was increased from 20°C to 110°C.
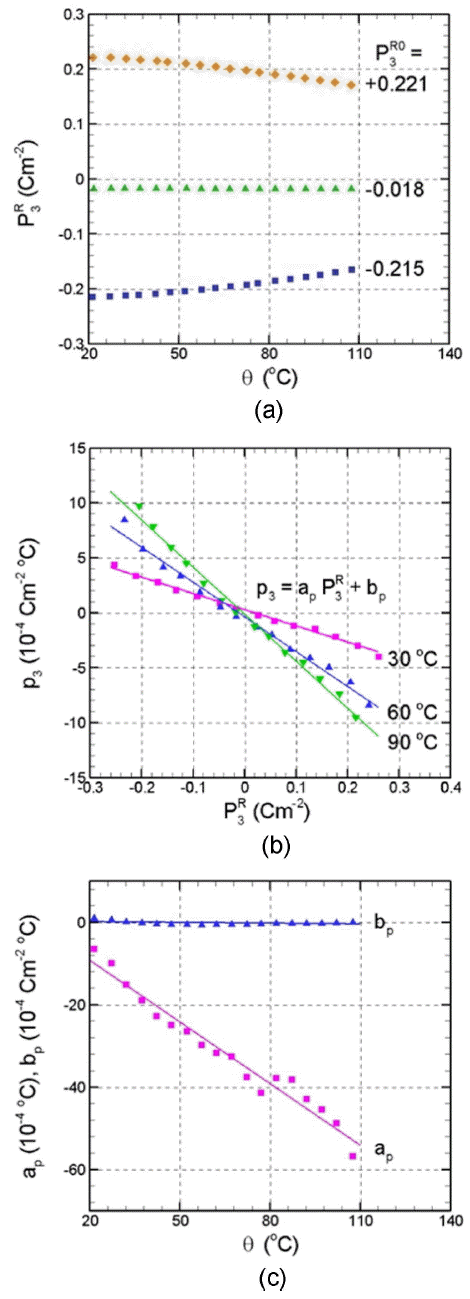
Changes in the ceramic specimen remnant polarization
P 3 R P 3 R 0 P 3 R 0
When the remnant polarization is near 0, or equivalently, when
P 3 R 0 = - 0.018 Cm - 2
The change in remnant polarization due to temperature is called the pyroelectric coefficient, and it is represented with p3. In this study, rather than assuming that the pyroelectric coefficient was constant throughout the temperature range from 20°C to 110°C, the pyroelectric coefficient was obtained for every 5°C interval. Fig. 2(a) shows the change in pyroelectric coefficient with the remnant polarization at constant temperatures, in the temperature range from 20°C to 110°C. Fig. 2(b) shows the pyroelectric coefficients obtained for the temperatures of 30, 60, and 90°C based on the remnant polarization. It can be observed that the pyroelectric coefficient data for constant temperatures can be fitted with single lines. Equation (1) below shows the expression for the line.
Here, aP is the slope of the line shown in Fig. 2(b) and bP is the value of the fitting line value when the reference remnant polarization is 0. The distribution of the values of aP and bP for the entire range of 20°C to 110°C is shown in Fig. 2(c). Interestingly, aP and bP can also be expressed as straight lines over the temperature. The following equations express the lines.
Here, aPθ and bPθ are the slopes of the lines shown in Fig. 2(c), and aP0 and bP0 are the intercept values of the lines at the vertical axis. Substituting Eq. (2) into Eq. (1) results in Eq. (3) below.
Using Eq. (3), the pyroelectric coefficient p3 can be calculated when temperature θ and remnant polarization
P 3 R
3.2. Changes in Thermal Expansion Coefficient and Remnant Strains During Temperature Increase
In this study, to compensate for the error in measured strain due to high temperature, the thermal expansion coefficient was measured first for the specimen using the invar specimen, then integrated to obtain the strain value, rather than using the temperature compensation curve provided by the manufacturer. In order to obtain the coefficient of thermal expansion of the specimen, the same strain gauges were attached to the ceramic and invar specimens, and then the thermal power from each gauge was measured as the temperature was increased. The equation for calculating the thermal expansion coefficient in the VISHAY manual13) is as follows.
Here, αS and αR are the coefficients of thermal expansion for the ceramic and invar specimens, respectively.
The αR value provided by the manufacturer was 0.75 × 10−6 °C−1. ɛG/S and ɛG/R refer to the thermal powers measured using the strain gauges attached to the ceramic and invar specimens, respectively. 2-axis strain gauges were used, and the thermal power values in longitudinal and transverse directions were measured to calculate the longitudinal and transverse direction thermal expansion coefficients α3 and α1, respectively, using Eq. (4). Δθ is the temperature range of the thermal expansion coefficient measurement.
Figure 3(a) shows the variation in the longitudinal and transverse thermal expansion coefficients α3 and α1 for the ceramic specimen calculated using Eq. (4), plotted versus the temperature. The figure shows the variation in the longitudinal thermal expansion coefficient α3 according to the temperature for the reference remnant strains +1.419 × 10−6, −151.7 × 10−6, and −458.2 × 10−6 among the total 14 reference remnant longitudinal strains
S 3 R 0 S 3 R 0
The integration is carried out as shown below for the remnant longitudinal and transverse strains
S 3 R S 1 R
Here, the Euler integration begins with the reference remnant longitudinal and transverse strains
S 3 R 0 S 1 R 0
Figure 3(b) shows the calculated longitudinal and transverse remnant strains. In Fig. 3(b), the largest applied electric field at the reference temperature was
S 3 R 0 = - 458.2 × 10 - 6
On the other hand, when
S 3 R 0 = + 1.419 × 10 - 6
For the case of
S 3 R 0 = - 151.7 × 10 - 6
Figure 3(c) shows the change in longitudinal thermal expansion coefficient for the constant temperatures of 30°C, 60°C, and 90°C, plotted versus the remnant strain. Interestingly, like the result in Fig. 2(b), the change in thermal expansion coefficient at constant temperature, when plotted versus the remnant state variables, can be fitted with a straight line. The slope aS3 and intercept bS3 values of the lines vary with temperature, and Fig. 3(d) shows the distribution over temperature. The slope and intercept data shown in Fig. 3(d) also show linear distributions, and the same method can also be used with the pyroelectric coefficient p3 data in Fig. 2(c) to express the slope and intercept as linear equations. Equation (6) can be obtained when the linear equations in Fig. 3(d) are applied to the linear equations in Fig. 3(c).
Here, aS3θ and bS3θ are the slopes of the lines in Fig. 3(d). When the temperature is 0, the intercept values are aS30 and bS30. The equations are similar to Eq. (3) for the pyroelectric coefficient, and the equation for the transverse direction strain
S 1 R S 3 R ( or S 1 R )
3.3. Governing Differential Equations and Empirical Formula
The pyroelectric coefficient p3 is the rate of change in the remnant polarization
P 3 R p 3 = d P 3 R / d θ
In Eq. (7), the ± sign on the right side is related to the directions of the specimen polarization and the applied electric field at the reference temperature. The + sign corresponds to when the electric field is applied in the positive direction to the specimen poled in the negative direction, and the − sign corresponds to when the electric field is applied in the negative direction to the specimen poled in the positive direction. This is a natural result. Using the definitions of the longitudinal and transverse thermal expansion coefficients, the governing differential equations similar to Eq. (7) can be obtained for the longitudinal and transverse strains
S 3 R S 1 R P 3 R , S 3 R S 1 R
Here, the dependent variable Y can be
P 3 R , S 3 R S 1 R Y 1 ( P 31 R , S 31 R , or S 11 R )
Here, I(θ) is expressed with Eq. (10) shown below.
(10)
In Eq. (10), erf(x) is the error function.
The temperature rise experiment was carried out using a new PZT specimen, and the analysis of the data revealed that the derived empirical equation (9) was the same as a previously derived equation. This shows that the process of establishing the governing differential equation can be generally applied to the nonlinear behavior of ferroelectric PZT materials.12)
3.4. Comparison of Calculated and Empirical Results
Figure 4 shows the changes in the remnant polarization
P 3 R S 3 R S 1 R P 3 R 0
Figure 4(a) shows the changes in remnant polarization. For the longitudinal and transverse strains, Fig. 4(b) shows the case when the reference remnant polarization was negative and Fig. 4(c) the case when the reference remnant polarization was positive. The experimentally measured values of
P 3 R , S 3 R S 1 R P 3 R , S 3 R S 1 R
However, to make an approximate calculation, it can be assumed that the remnant state variables vary at constant rates with the temperature. Comparisons of the calculated and measured values shows that they are in good agreement with each other for all states of reference remnant polarization. Thus, it is concluded that Eq. (9) can be used to predict the macroscopic changes in polarization and strains of ferroelectric specimens, when temperature is increased.
The rates in the changes in the measured values of
P 3 R
The predicted values of the pyroelectric coefficients can be obtained using Eq. (3) for given temperature and remnant polarization, and the calculated pyroelectric coefficient values are represented by solid curves in the same figure. It was observed that the calculated and experimental results were in relatively good agreement for the five reference remnant polarizations.
The thermal expansion coefficients obtained directly from experiments with the invar specimen are represented by solid curves in Figs. 5(b) and (c). In the same figures, the calculated values of thermal expansion coefficients from Eq. (6) are plotted by symbols. Like Figs. 4(b) and 4(c), Fig. 5(b) corresponds to the case where the reference remnant polarization was negative, and Fig. 5(c) corresponds to when it was positive. It was found that the calculated and experimental results were in relatively good agreement for all the reference remnant polarizations in the figure.
As mentioned in Fig. 4, if the changes in the remnant polarization and remnant strains are linear in relation to temperature for the relatively small temperature range from 20°C to 110°C, the pyroelectric and thermal expansion coefficients of Fig. 5 have to be assumed to be constant in the given temperature range. However, as can be observed in the figure, the thermal coefficients varies with the temperature, and therefore, the changes in thermal coefficients with temperature need to be included in the construction of an empirical modeling equation.
Lastly, the switching processes induced by an electric field were compared for different temperatures.
The research method used in this study was to investigate the nonlinear behavior of materials by observing changes in the remnant state variables, which represent the macroscopic behavior of the ferroelectric specimen. Then, the variations in the remnant polarization
P 3 R S 3 R S 1 R
In this study, the changes in the state variables when the temperature of a ferroelectric specimen switched by an applied electric field at the reference temperature was increased, were investigated. Comparisons of the measured changes in the state variables during temperature rise and the predictions by the developed empirical formula showed a good agreement, as had been observed by experiment.12)
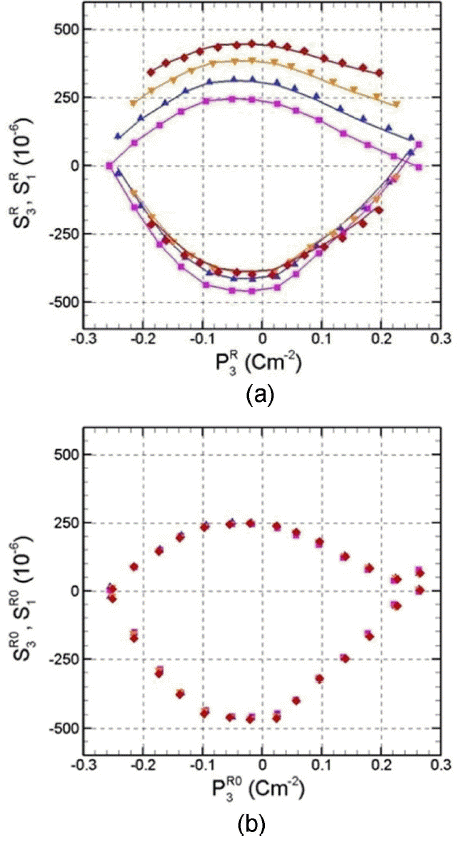
First, the state variables measured for temperatures of 20°C, 50°C, 80°C, and 110°C are shown in Fig. 6(a), using square, triangle, inverted triangle, and diamond symbols, respectively. Also, the reference remnant variable values at 20°C were substituted into Eq. (9) to obtain the corresponding remnant variable values for 50°C, 80°C, and 110°C.
Figure 6(a) shows the calculated results in line form for each temperature case. In the figure, it can be observed that the prediction of the remnant strain variation with regard to the remnant polarization density is almost equivalent to the marked measurement results for the three temperature cases. By substituting the remnant state variable values measured for temperatures 50°C, 80°C, and 110°C in Eq. (9), the state variable values at reference temperature were obtained.
Figure 6(b) shows the reference remnant variables measured at 20°C, and the calculated reference remnant state variable values for three high temperatures. The reference remnant strain variations over reference remnant polarization were almost the same for all temperatures. This implies that the relationships between the reference remnant state variables are the same when switching is caused by electric field.
In summary, it can be seen in Figs. 6(a) and (b) that the relationships between the macroscopic state variables are the same at different temperatures when switching is induced by an electric field. This means that the switching process by electric field is the same at different temperatures from the macroscopic point of view. If the microscopic domain structure corresponds to the macroscopic state variables on a one-to-one basis, this study shows that the process of change in the microscopic domain structure during switching by electric field is the same for different temperatures.
4. Conclusions
At the reference temperature, an electric field is applied in a direction opposite to polarization for a poled PZT ceramic specimen. After applying electric fields of 14 different magnitudes at the reference temperature, the temperatures of the ceramic specimen and invar specimen were increased from 20°C to 110°C. During the temperature increase, the remnant polarization and thermal expansion coefficient were measured. Using the measured values, differential equations governing the behavior of remnant polarization and remnant strains during the temperature rise were derived.
The empirical formula obtained from the governing differential equations was used to predict the changes in remnant polarization and remnant strains during temperature increase, and these values were then compared with the experimental results. The predicted and experimental results were in very good agreement for all the initial conditions. The predicted and experimental results for the pyroelectric and thermal expansion coefficients were also in good agreement with each other.
Finally, the switching processes due to an electric field at different temperatures were compared using the remnant state variables, and it was found that the switching processes by an electric field for the tested temperature range were equivalent, from a macroscopic state variable perspective.
The results of this study are similar to the results of a study conducted for a different PZT specimen, and they verify the validity of the derived empirical formula derived in this study.12)