1. Introduction
Thermoelectric materials that recover waste heat and transform it into electricity or vice versa have attracted much attention because of their potential to help solve the current global energy crisis. Even though, up to now, thermoelectric materials have mainly been used in niche markets such as small refrigerators, a cooling device for laser diodes and cooling seats in automobiles, there have been many efforts to widen the applications of thermoelectric materials by enhancing their properties. The thermoelectric performance of the materials is characterized by the so-called dimensionless figure of merit, ZT=S2σT/κ, where S is the Seebeck coefficient; σ is the electrical conductivity; κ is the thermal conductivity, and T is the absolute temperature. 1,2) Conventional thermoelectric materials show ZT~1 at room temperature.1,2) Recently, the enhancement of ZT with ZT > 1 has been reported by many researchers. Heremans et al. reported that the value of ZT was 1.5 at 773K in Thallium doped PbTe due to the local distortion of the density of states and the resulting enhancement of the Seebeck coefficient.3) Pei et al. reported a ZT value of 1.8 at about 850K in Na-doped PbTe1−xSex alloys due to convergence of many valleys in the valence bands.4) Other improvements of ZT in the PbTe alloys have been reported in many instances.5) Nevertheless, the developed materials have limited use and commercialization due to environmental, economic and technical limitations including toxic elements in the materials, high cost elements in the materials, and a lack value for the ZT, respectively.
To design and discovery novel thermoelectric materials with high thermoelectric performance, computational simulations of the thermoelectric properties could have an important role in discovering novel materials as well as in guiding experiments and understanding the results. The computational simulations of three properties, the Seebeck coefficient, the electrical conductivity, and the thermal conductivity, have been a long-standing interest to many researchers. The core properties such as the band structure and the density of states, in calculating the transport properties, can be obtained with well-established computational tools. On the other hand, the computational tools for estimating the transport properties were recently established and released to the public. This review covers the latest advancements in computational simulations of thermoelectric properties mainly focusing on the first-principles calculations with the aim to increase attention on thermoelectric technologies in other researchers in computational materials science and highlight potential routes for the discovery of new thermoelectric materials. As a model case, this review presents the results of the electrical and thermal properties of Bi2Te3 and Si in detail.
2. Electrical Transport Properties: Seebeck Coefficient and Electrical Conductivity
The computational simulations for electrical conductivity and the Seebeck coefficient can be done with the first-principles calculations and the Boltzmann transport equation. The code BoltzTrap is the most widely used simulation program for electrical properties.6) This code was first written to use the eigen energy from the WIEN2k code.7) Furthermore, other codes for the first-principles calculations such as VASP and Quantum Espresso can also be used to produce the eigen energy for which the correspondent interface program was also developed.8-10) The BoltzWann code is also available to evaluate electrical transport properties with a maximally-localized Wannier function basis set.11)
Charge transport occurs when an electric field, and/or thermal gradient is present, and this phenomenon can be described as shown below:12)
where J is the charge flux; e is the electronic charge; f is the charge distribution; σ is the electrical conductivity; E is the electric field and v is the charge velocity. Namely, if we know the distribution of the charge with respect to time and space, the flux of the charge can be determined. The charge distribution as a function of time can be described as follows: 12)
where r is the position of the electrons; p is the momentum and the subscript c means collision. Thus, the above equation indicates the change in charge distribution after collision. And then, the relaxation time approximation is assumed here.
From equation (2)~(4), we can obtain
and when we replace (1) with equation (5), the electrical conductivity can be described as
This equation can be rewritten as the tensor form within electronic structure calculations given as
where Ω is the unit cell volume; e is the carrier charge; ɛ is the band energy; N is the number of k-points used in the calculation; f0 is the Fermi-Dirac distribution function; τ is the relaxation time; ν is the group velocity of charges and δ is the delta function.6,13) The subscripts k and n mean the crystal momentum and the band index, and the velocity, ν, can be estimated from the band structure with the following relationship:
where ℏ is the reduced Planck constant.
When a temperature difference is present, the total electric field is different from equation (1) due to the field originating from the Seebeck effect, and then, equation (1) is changed to
And the heat flux (q) produced from the temperature difference can be described as
where Js is the entropy flux. Both equations (9) and (10) are called the Onsager relationship.14) Using equations (9) and (10), we can obtain the Seebeck coefficient and electronic thermal conductivity (ke) obtained from the band structure calculation, and the results are shown below:6,13)
where μ is the chemical potential, and kB is the Boltzmann’s constant. From the equations above, we can identify that the electrical conductivity, Seebeck coefficient, and electronic thermal conductivity can be directly estimated from the band structure. Only one parameter we do not know yet is the value of the relaxation time. If we assume that the relaxation time varies less within the energy window of interest, namely, assuming that the relaxation time is constant, the Seebeck coefficient can be derived from the band structure without any fitting parameter because the constant relaxation time in the numerator and denominator disappears. Of course, the relaxation time is dependent on the band energy in real materials. Most codes for electrical transport properties such as BoltzTraP and BoltzWann evaluate the properties with a constant relaxation time approximation and with energies of bands obtained from very fine meshes in the reciprocal lattices.
2.1 Case: Bi2Te3
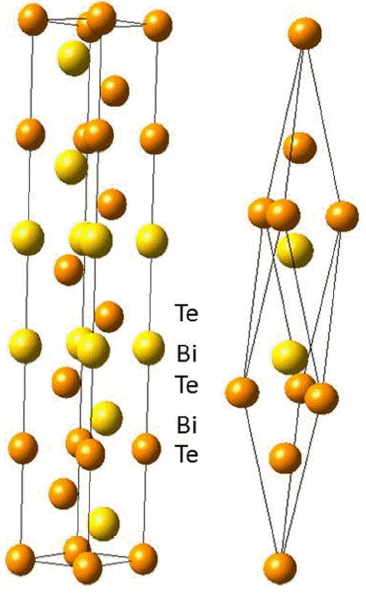
Bi2Te3 is a well-known thermoelectric material for room temperature and is used in commercially available thermoelectric modules. Therefore, there are many reports on the electronic structures of Bi2Te3, and the results of transport properties simulations have been reported since the early 2000’s.15-29) The crystal structure of Bi2Te3 is shown in Fig. 1, and the space group of the crystal structure is R m.30) The quintuple sequences of Te(1)-Bi-Te(2)-Bi-Te(1) are stacked along the c-axis in the hexagonal cell, where Te(1)-Te(1) has weak van der Waals bonding, and the others have a mixture of covalent and ionic bonding. It is well known from experiments that the transport properties show anisotropic features. The electrical and thermal conductivity are larger along the basal plane than along the trigonal axis which originates from a layered-like crystal structure of Bi2Te3. The major defects in Bi2Te3 are antisite defects which are responsible for carrier concentration.31)
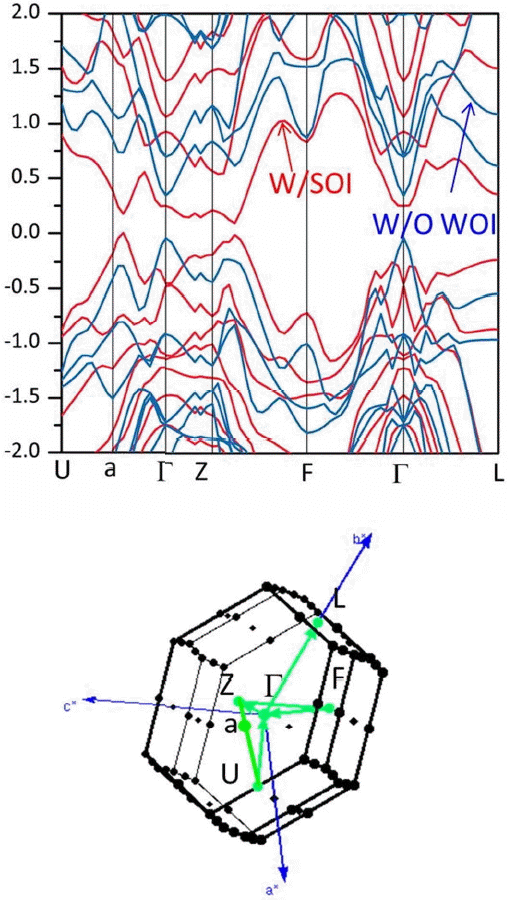
The characteristic electronic structure of Bi2Te3 and its related compounds such Sb2Te3 and Bi2Se3 are listed in Table 1, and the band structure of Bi2Te3 is also shown in Fig. 2. The band structure was obtained with the WIEN2k code with the following parameters: RMTKMAX=10, RMT=2.5 a.u., 72 k-points 3 in irreducible Brillouin zone and PBE-GGA.7,32) It is clearly seen that the spin-orbital interaction (SOI) should be included in the calculation to produce the exact number of carrier pockets, the position of the band edges, and the band gap. Without the SOI, the conduction band edge and the valence band edge are located at Γ, whereas they move to the symmetry lines with the SOI. The discrepancy between reports may originate from the differences in the lattice parameter used in the calculations and in the simulation codes and parameters such as the exchange-correlation potential and the use of van der Waals interactions.
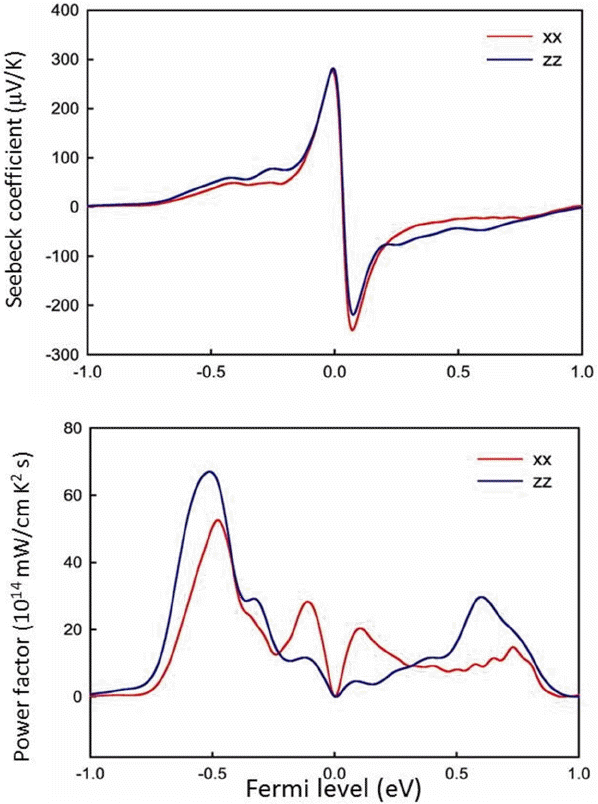
The electrical transport properties of Bi2Te3 have also been obtained with the Boltzmann transport equations shown in Fig. 3. The BoltzTraP code was used to evaluate the transport properties. In evaluating the Seebeck coefficient, the relaxation time is assumed to be constant (10−14 s), and the rigid band assumption is used to calculate the properties with respect to the Fermi energy. The anisotropic property is well seen in the power factor (S2σ), which is due to large anisotropic electrical conductivity, whereas a relatively less anisotropic Seebeck coefficient was evaluated. Experimentally, (Sxxx − Szz)/(Sxxx) < 0.1 and
σ x x σ z z = 4 ~ 7 m d = N v 2 / 3 ( m 1 m 2 m 3 ) 1 / 3
2.2 Beyond the Constant Relaxation Time Approximation
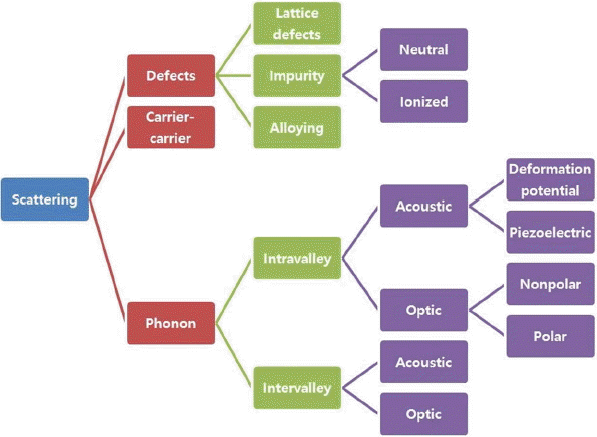
The constant relaxation time approximation can be used for the Seebeck coefficient, but evaluation of the electrical conductivity should be done with some value of the relaxation time, for which we can fit the obtained electrical conductivity with the experiment and then acquire the value of the relaxation time. However, we need to overcome this obstacle in materials design or materials discovery. As shown in Fig. 4, there are various scattering mechanisms including deformation potential acoustic phonon scattering, ionized impurity scattering and so on. Among these scatterings, polar optic phonon scattering and ionized impurity scattering can be partly evaluated with the obtained parameters from the first-principles calculations such as the band gap, effective mass, high frequency and static dielectric constants. 37) The strength of the electron-phonon scattering can be also estimated in part from the first-principles calculations. For example, metals such as Cu and Ag have electron-phonon scattering as the dominant scattering mechanism of the electrical conduction at room temperature and above. In this case, the electrical conductivity can be also described as
Here, θD is the Debye temperature; the constant αel−ph is proportional to
λ t r ω D / ω p 2
where
F t h ≅ ( 1 - 0.0038 θ D 2 τ 2 ) - 1
3. Thermal Conductivity
In this section, we briefly summarize the method to calculate the phonon thermal conductivity of thermoelectric materials by using the first-principles calculations. The thermal conductivity is composed of the electronic thermal conductivity and phonon thermal conductivity. The electronic thermal conductivity is computed from the electronic transport tensor by equation 12 shown already. Phonon transport properties are calculated based on the Boltzmann Transport Equation (BTE) combined with the Relaxation Time Approximation (RTA).38,46) Phonon frequencies and phonon life times are computed based on the supercell approach calculating the inter-atomic force constant.47-53) The inter-atomic force constants(IFC) are obtained from the density functional theory. Then, 2nd and 3rd order phonon Hamiltonian is constructed. Then, the phonon life times and phonon thermal conductivities are calculated using the many body perturbation theory. Recently, the phonon thermal conductivity codes PHONO3PY and ShengBTE have become public to researchers.54-58) Herein, the phonon life times and thermal conductivities are computed with the PHONO3PY code.54-56)
To calculate the phonon thermal conductivity, we have to calculate the phonon lifetime. When the phonon Hamiltonian is only composed of 2nd order terms, there is no phonon scattering, and the phonon thermal conductivity should be proportional to the number of phonon channels. However, due to the anharmonicity in atomic potential surfaces, the phonon Hamiltonians are expanded with 3rd or higher order terms written as H = E0 + K + H2 + H3 + ···, where EO, K, Hn are the ground state total energy, the atomic kinetic energy, and the n-body crystal potential terms.54-56)
Note that HHarmonic = K+H2 is the harmonic Hamiltonian for the phonon and written as a sum of harmonic oscillators,
H H = ∑ λ ℏ ω λ ( 1 2 + a ^ λ + a ^ λ ) H 3 = ∑ λ λ ′ λ ″ ( a ^ λ ′ + a ^ - λ ′ + ) ( a ^ λ ″ + a ^ - λ ″ + )
For the Si FCC structure, there are two Si atoms in the primitive cell. However, to compute the 2nd and 3rd order IFCs, we need to generate many supercell configurations containing atomic displacements. For the 2nd order, only single atomic displacements are needed. However, for the 3rd order, two atomic displacements are needed. If we consider the (4 × 4 × 4) supercell of Si FCC, then there are N = 128 atoms. Then, there are 3N displacements for one Si. Because we need two atomic displacements, there are huge numbers of displacement configurations exceeding 106 (since N = 128, 3N × 3N = 9N2 = 147,456). Fortunately, due to the symmetry operation,54-57) the number of configurations can be reduced. In the PHONO3PY code, there are only 416 configurations. In the case of the Bi2Te3 hexagonal unit cell with 15 atoms, the number of configurations is very large (5108) due to less symmetry in the lattice of Bi2Te3. For low symmetry materials, there will be too many configurations. Then, it will be a good idea to reduce the number of configurations to cutoff the large distance displacement configurations. For Si, the evaluation of 5th neighborhood or higher neighborhood interactions changes the phonon thermal conductivity only negligibly.
Before generating displacement supercell configurations, one needs to check whether the primitive or unit cell is fully relaxed. Because the IFC analysis needs the atomic forces, the force noise is very harmful in the calculation of the phonon modes and 3rd order calculations. Here, the atomic forces for Si and Bi2Te3 are smaller than 0.00002 eVÅ−1. Also note that the phonon thermal conductivity is very sensitive to the lattice parameters, especially for thermoelectric materials.59) Here, we fix the lattice parameter of Si to be 5.47 Å from the PBE calculations and those of Bi2Te3 to be a = 4.3835 Å and c=30.487 Å from the experimental values. Also note that the choice of exchange correlation energy will alter the result of the phonon thermal conductivity.
We calculate the IFCs using the Si (4 × 4 × 4) FCC supercell and Bi2Te3 (4 × 4 × 1) hexagonal supercell. They contain 128 and 240 atoms. And the corresponding IFC supercell configuration numbers are 416 and 5108. To reduce the computational cost, we use the Γ point calculation for the electron Brillouin zone integration. We choose the PREC = ACCURATE tag for the VASP calculation and self-consistent-field (SCF) loop criterion of EDIFF = 1 × 10−8 eV following the suggestion of Togo.57) As a tip, we suggest storing the electronic wave function for the perfect non-displaced supercell. Using it, the DFT force calculation time is reduced in half. For us, we have 30 nodes, and each node contains 12 cores. For Bi2Te3, because each configuration takes about 400 to 500 seconds, the total calculation time is about 9 days. If we use more k-point, the computational time can take longer than several weeks or a month.
The 3rd order phonon process then can be calculated using the 2nd and 3rd order IFCs. The PHONO3PY code gathers the atomic forces for various configurations. The next time consuming step is to calculate the phonon self-energy. The phonons are scattered by three phonon processes. In this work, we used the phonon reciprocal lattice q mesh of 11 × 11 × 11 for Si and Bi2Te3. Because there are 113 q points, there are 113 × 113 × 113 three phonon processes. Note that it is a very time and memory consuming step if the unit cell is large, and the q mesh is fine. For the Bi2Te3 case, in the irreducible Brillouin zone, there are 146 grid points. Each q grid point phonon self-energy calculation is done in one node. For us, the total time of the calculations was about 4 days. If the unit cell is large, the calculation can crash, or the calculation time will be very long.
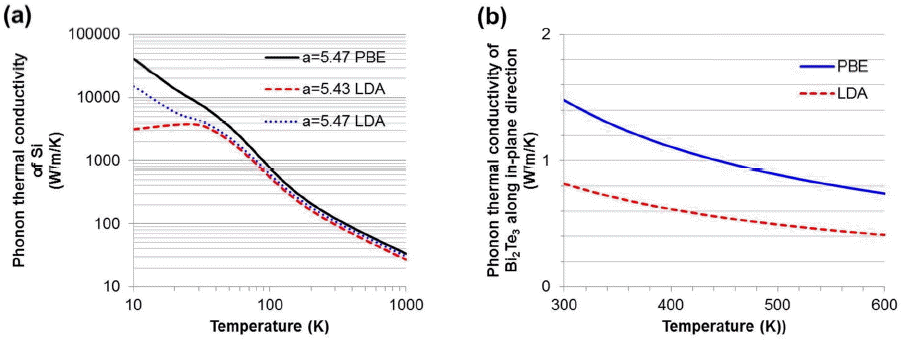
Then, the phonon thermal conductivity is obtained by gathering all phonon self-energies. Fig. 5(a) and (b) represent the phonon thermal conductivities of Si and Bi2Te3 with various calculation methods. We consider three different cases: PBE with a lattice parameter a = 5.47 Å, LDA with a = 5.47 Å and LDA with a = 5.43 Å. We find that the room temperature (300K) phonon thermal conductivity is 122 W/m/K for the PBE with a = 5.47 Å. The differences among the phonon thermal conductivities are about 20 - 70% for temperatures ranging from 10 to 100 K. When the temperature is larger than 300 K, the difference becomes less than 10% for PBE and LDA. However, for Bi2Te3, the choice of exchange-correlation energy is very sensitive to the thermal conductivity results. When we compared it to experimental results, the PBE results seems to be more reliable.
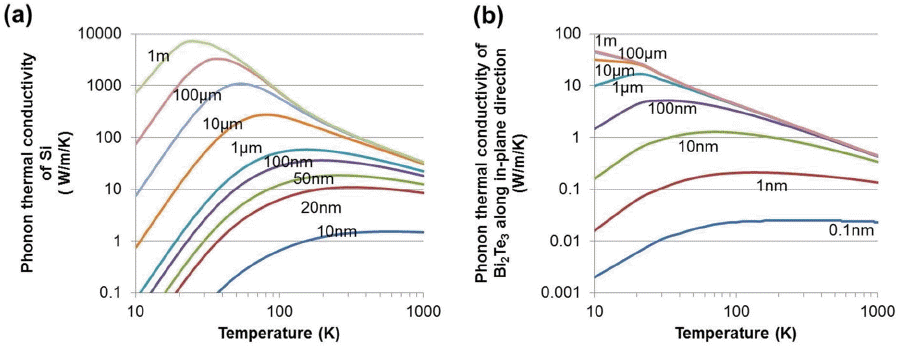
Next, we examine the boundary effects on the phonon thermal conductivities, especially for PBE calculations shown in Fig. 6. The relaxation time of the phonon is modified following Matthiessen’s rule written as
1 τ = 1 τ P h o n o n + 1 τ B o u n d a r y 1 τ P h o n o n 1 τ B o u n d a r y 1 τ B o u n d a r y = v g L
For Bi2Te3, the phonon thermal conductivity with the boundary mean free path is examined. The phonon thermal conductivity curves are fitted using the following equations κphonon = κ0Tα, and the prefactor κ0 and exponent α are summarized in Table 3. The phonon thermal conductivity of Bi2Te3 at 300 K is very small (1.4 W/m/K) and when there is no boundary scattering, the phonon thermal conductivity is proportional to the inverse temperature (T−1). When the boundary scattering length is shortened, the phonon thermal conductivity is decreased, and the temperature dependency is weakened. The most effective boundary mean free path size is smaller than 100 nm. Note that when L is between 100 nm and 1 μm, the reduction of thermal conductivity is only 10 %. However, when 10 nm boundary scattering is introduced, the phonon thermal conductivity is severely reduced to 50%. It is thought that, in Bi2Te3, the smaller sized nanostructured bulk is needed for a classical thermoelectric material such as Bi2Te3. When we considered the average electron mean free path of Bi2Te3 (known to be about 10 - 20nm), the optimal nanostructuring size is about 10 - 20 nm to minimize the reduction of electrical conductivity. A similar result is also found for PbTe.63,64)
4. Utilization of Computational Simulation in Discovering Novel Thermoelectric Materials
Based on the first-principles calculations, all thermoelectric properties can be evaluated with the assumption that the relaxation time is constant so that we can screen candidates to discover novel thermoelectric materials. Madsen who developed the BoltzTraP code reported the screening procedures for thermoelectric materials containing the Sb element.65) Gorai et al., reported on the computational exploration of a binary compound of the A1B1 chemical space for thermoelectric performance.66)
5. Conclusions
We have shown that thermoelectric properties such as the electrical conductivity, the Seebeck coefficient, and the thermal conductivity could be evaluated from the electronic band structures and the inter-atomic force constants both obtained from the first-principles calculations within the density functional theory. It was shown that a combinational use of the simulator of electronic structures with the electrical Boltzmann transport equation solver and phonon calculation packages can give quantitative and comparative results. However, there are also obstacles to be overcome. The effect of scattering from various sources in existing real materials could not be involved in most calculations so that a few assumptions are used such as the relaxation time is constant. Despite this rigorous assumption, the computational simulations can be used to screen materials to discover novel thermoelectric materials. With the improvement of computational power, a new method for treating scattering is being developed so that a time will come in the near future when we can design thermoelectric materials with less approximation.