1. Introduction
In this era of the fourth industrial revolution,1) numerous attempts have been made to apply data-driven optimization schemes to manufacturing processes in materials science and various industries. Because of recent developments in information technology, it is now possible to achieve fast and reliable optimization of various manufacturing processes, even for highly complicated interconnected processes. However, gathering a sufficient number of reliable data sets related to the targeted manufacturing processes remains a critical issue for successful optimization. Once the required amount of big data for a manufacturing process has been collected, it can be applied machine learning algorithms2) to analyze and optimize the parameters being considered. Artificial intelligence (AI) is a smart algorithm for performing certain kinds of complex jobs by utilizing big data and fast computers to mimic human intelligence. After a primitive concept of artificial intelligence was proposed by Samuel in 1959, various evolutionary algorithms were developed, including recently proposed deep learning algorithms based on neural networks.3) Once a sufficient amount of big data is collected, the fastest and most reliable optimization method now seems to be available for a wide range of industrial applications.
In the manufacturing process in the ceramics industries, various individual manufacturing steps such as material synthesis, mixing, forming, drying, and sintering must be optimized. To apply the optimization scheme using a machine learning algorithm, a sufficient amount of data for the individual processes must be provided. It is, however, difficult to collect enough data for the actual manufacturing process. Thus, some alternative approaches have been developed to generate “virtual data,” such as analytic formulas, computer simulations, image processing, and artificial intelligence. In material science, it is becoming commonplace to employ the big data approach to new material design using computer simulations, e.g. density functional theory.4)
In this study, we used a stochastic mathematical model to generate a virtual image set of two-dimensional cracks created in ceramics manufacturing processes, and the similarity of the images was quantitatively determined by using a simple cosine similarity factor. Although additional geometric parameters for the generation and comparison of crack patterns are available, in this work, to demonstrate how to generate big data sets of crack images, we focused on a few geometrical parameters to demonstrate the algorithm. Other parameters are left to be addressed in future studies.
2. Cracks Patterns of Ceramics
One of the most widely applicable ways to analyze the generation mechanism of faults in ceramic forming processes is to use artificial vision data.5) It is difficult to achieve faultless ceramic products due to fault generation, especially thermomechanical deformation, which is inevitable in ceramic forming processes. Major faults of ceramic products are various types of cracks generated on the surfaces.6)
To apply machine learning to optimize these forming processes, it is necessary to first have a sufficient number of images with faults. In this study, we generated virtual data for the optimization process, which is the first step in categorizing the patterns of cracks in terms of geometric parameters, i.e., length, thickness, and depth. It is noted that the individual images were still highly diverse, even with the same geometric parameters.
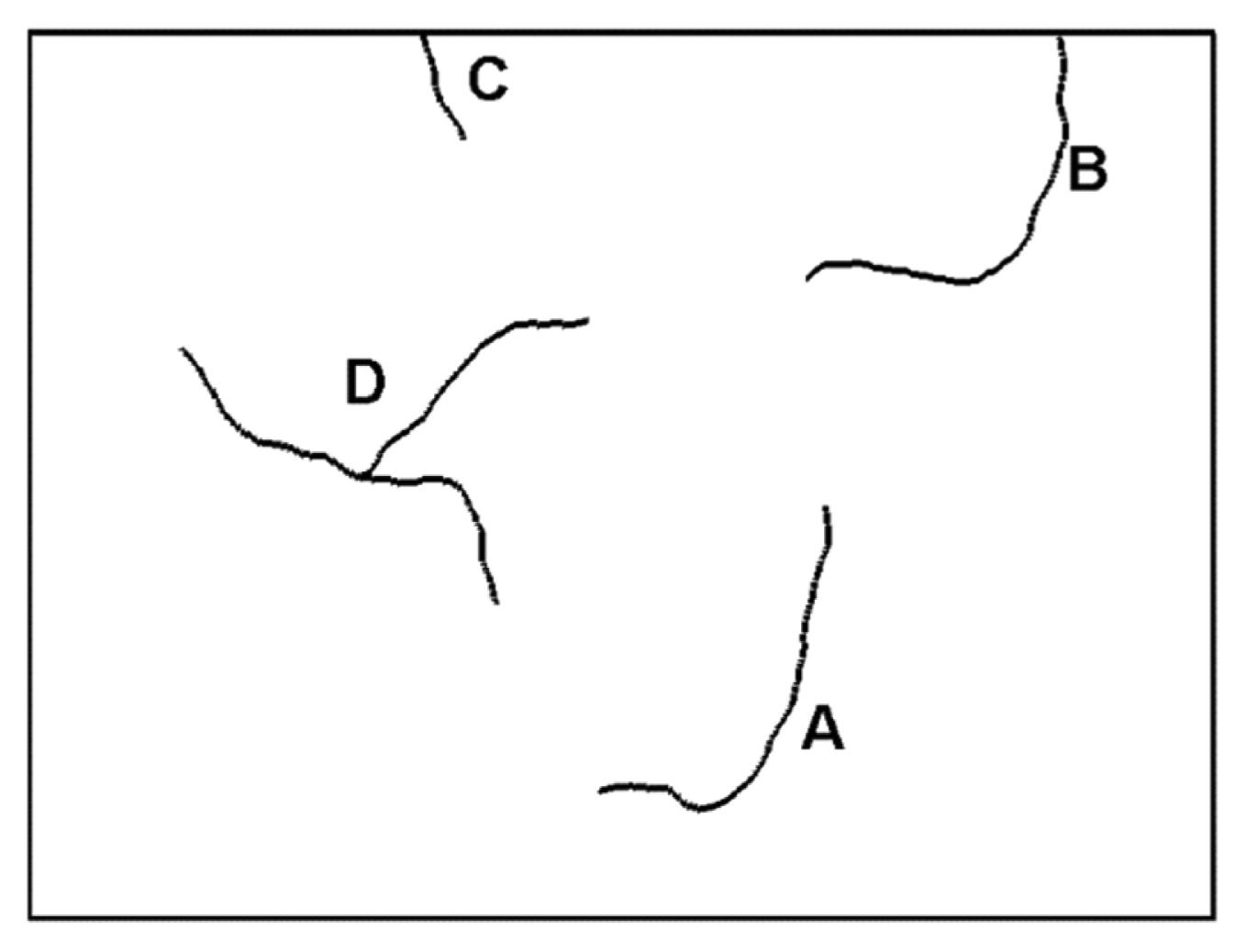
Cracks on the surfaces of ceramic products are qualitatively and quantitatively diverse. Fig. 1 shows cracks on the surfaces of a polycrystalline ZnO ceramic, along with some impurities and voids.7,8) Fig. 1(a) shows a few simple types of cracks and Fig. 1(b) shows more complicated types of cracks, such as Y-shaped cracks where two simple cracks meet. Cracks with larger widths are usually deeper. In Fig. 1(b), crack A stays inside the grain and crack B meets the grain boundaries; this may occur because of the thermal stress that arises from polishing. Crack C forms near or on the grain boundaries. The cracks show diverse formation according to the average grain size and the microstructure, which are highly dependent on the manufacturing process parameters, such as the sintering temperature profile.
The production of ceramics usually includes sintering and pressing, during which temperature can control the average grain size and microstructure and also generate cracks. Polishing can also cause thermomechanical deformation, and the chemical etching process may produce cracks on the surfaces induced by thermal expansion and chemical reactions, as shown in Fig. 1. Therefore, a variety of crack patterns originate from many different processes, and these patterns need to be well categorized to be analyzed in machine learning. Then, the AI algorithm enables us to efficiently determine the optimal conditions for manufacturing processes to minimize cracks.
By imposing some conditions or constraints on the algorithm, such as uniform step length or directional angle, we may produce more or less predictable crack paths. However, realistic cracks on the surfaces of ceramic products exhibit unpredictable paths (caused by unidentified hidden variables), and therefore a stochastic model is needed to make the realistic “virtual” cracks normally observed in the manufacturing process.
The generation model is set up for a specifically targeted process. Big data for ceramic crack patterns may include a large amount of categorized data according to predefined aspects, i.e., the number of cracks, the length of each crack, a total length of the cracks, and whether a crack meets the edges. By varying the random seeds of the random walk algorithm, we produced a large amount of virtual vision data for the analysis. To control the uncertainty of the stochastic approach, the limits of certain parameters were controlled. In this study, we categorized a big data set for cracks on ceramics according to the above aspects and generated the “virtual” cracks using the random walk algorithm.
3. Random Walk Algorithm
In statistical mechanics, there are a few path-finding problems. The traveling salesman problem, Brownian motion, and the random walk belong to this category. The well-known traveling salesman problem is to simply find the shortest path visiting all interconnected cities only once. Brownian motion describes the motion of gas molecules by the diffusion process.9) The random walk is a sequence of steps in a stochastic pattern according to a time variable either in a lattice or in a continuous space. Brownian motion is a special case of the random walk with a continuous time limit.10)
To generate virtual data for the ceramic forming process, a mathematical model, i.e., the random walk algorithm, was employed in this work. This stochastic model is a reliable way to describe complicated patterns of cracks in ceramic surfaces with various faults, similar to that shown in Fig. 1. In statistical mechanics, the random walk algorithm produces an arbitrary path, such as Brownian motion describing the dynamic motion of free atoms. In this random walk algorithm, to describe the motion of a free atom, the moving distance and the change of the moving direction are rather randomly selected with few constraints at each time step. The resulting crack patterns after some amount of time are similar to cracks under certain constraints.
In some previous work, a few attempts have been made to introduce a self-affine fractal model11,12) to describe patterns of crack initiation and creation and the Voronoi tessellation model13,14) for polycrystalline microstructures. They are not quite efficient enough to obtain realistic images of crack patterns. In this work, however, we focused on simple one-dimensional crack patterns by using the random walk algorithm.
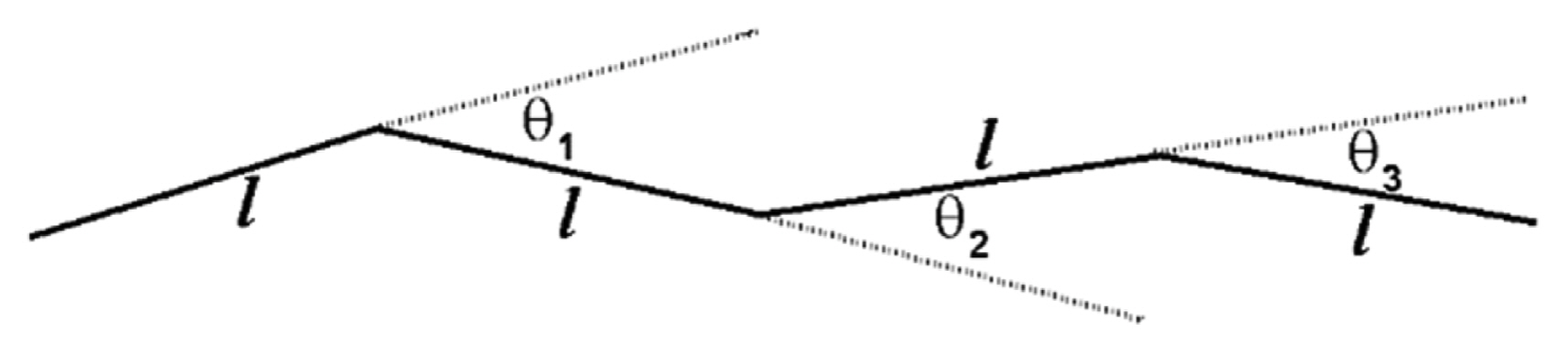
To generate virtual images of cracks on the surfaces of ceramics, we adopted the random walk process with discrete time steps in a continuous two-dimensional space. In general, the step length and the direction of each step can be arbitrary. However, we needed to impose some constraints on the process in order to produce certain regularities to imitate real cracks, as shown in Fig. 1. Fig. 2 shows the generating process of the random walk algorithm adopted in this work.15) The length of each step, denoted as l, was uniform and the change in direction was confined to within a specific angle. That is, the change in direction was set to be. Then, we made crack images of ceramics by continuing these steps, with the following criteria to stop the process. One criterion was the number of maximum steps Nmax, which confined the length of the crack. When the number of steps reached this number, the random walk process ended. Another criterion was the meeting of one crack to another crack or to an edge of the boundary. In these cases, the random walk process also ended. Using these relatively simple constraints in this numerical model, we generated a variety of realistic cracks on the surfaces of ceramics by varying the parameters, such as and Nmax, in a stochastic manner.
4. Results and Discussion
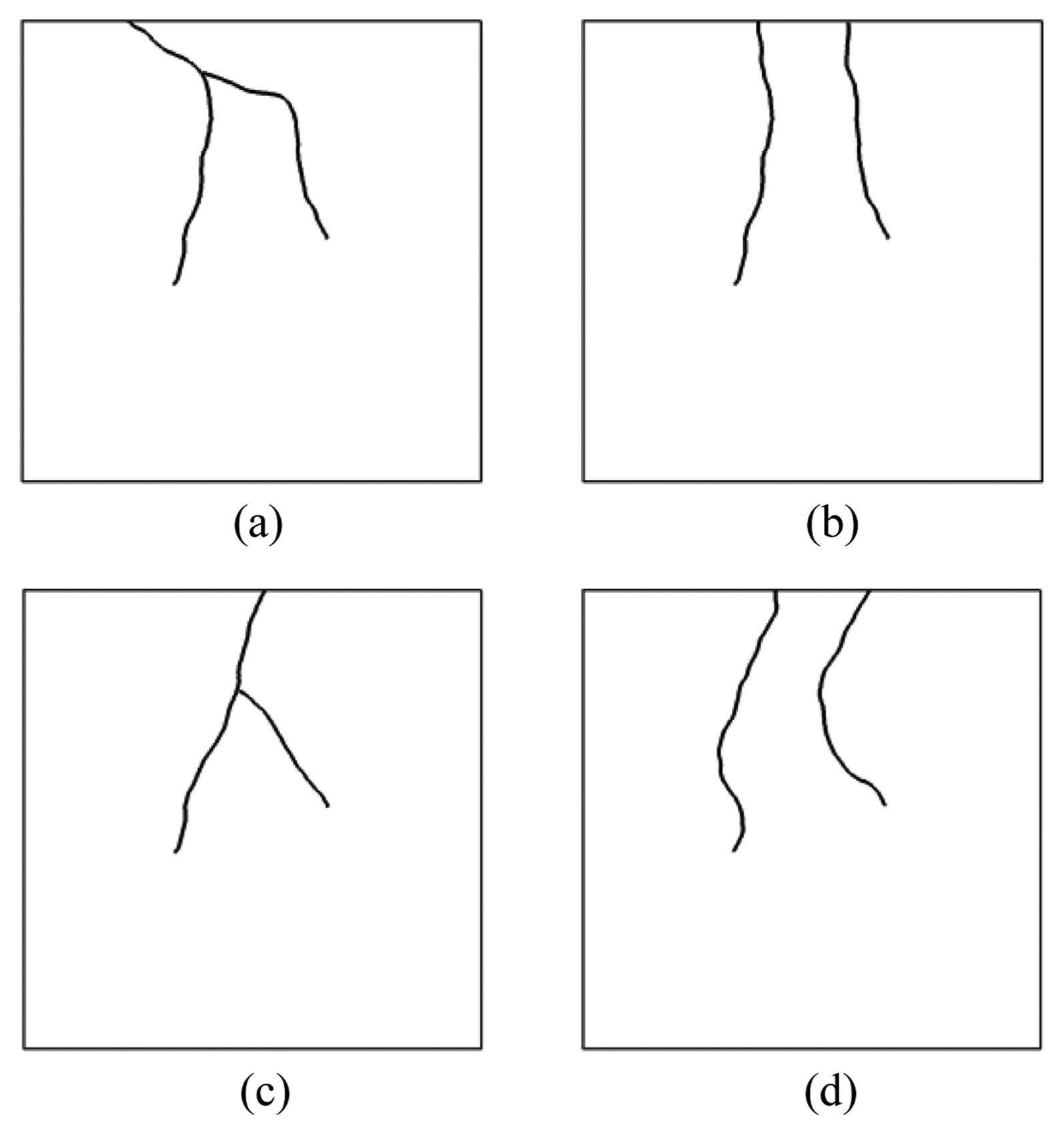
Using the random walk algorithm to generate cracks in a two-dimensional ceramic model produced various types of cracks, which are shown in Fig. 3. In Fig. 1, there are a few single cracks, some meeting the edges of the model while others did not. Some cracks are Y-shaped and composed of two cracks. The rectangular domain size of the ceramic model Lx × Ly was 640 × 480 and the number of cracks was five. The number of steps, Nmax, was 250, and the length of each step l was 1; hence, the length of each crack was 250 or less. In order to smooth the curves of the cracks, we set the maximum change of direction to be rather small, = 10°. For each crack, the position of the beginning point was randomly selected, and the random walk process continued to make the steps until it reached the specified criteria, i.e., where the number of steps N = Nmax and the cracks met other cracks or the edges of the model. In Fig. 3, crack A has a length of 250, crack B is shorter than A, and crack C is the shortest. Crack D is composed of two cracks, which is shown in Fig. 1(b). The cracks produced by the random walk process, shown in Fig. 3, closely resemble real cracks on the surfaces of ceramics, shown in Fig. 1. By adjusting the parameters of the algorithm, one can make cracks more realistic.
The virtual data sets for generating images of cracks on the surfaces of ceramics can be ordered in a systematic manner. For example, suppose we have up to five cracks on the model; then we can categorize the data simply by three parameters, i.e., the number of cracks, the length of each crack, and a total length of the cracks. This data format is shown in Table 1, along with the model number. Even though we considered three parameters in this work, our model can be generalized to include more quantitative and qualitative properties, such as the thickness of each crack, whether a crack touches the edges of the model, or whether it is an isolated single crack or two or more cracks combined.
The resulting crack images were plotted on a continuous map, and we simply converted the results to images on a digital map with a size of 640 × 480. Usually, the big image data obtained for the ceramic products had quality and quantity information on the cracks with the image files. An image file is digitized by converting it to a large number of pixels. That is, each pixel is assigned an RGB value for a color image or a grayscale value for a black and white image, with the value ranging between 0 and 255. For our case, for simplicity, we assigned a value of 0 or 255 to each pixel, and hence we had 640 × 480 data points that were either 0 or 255.
It is necessary to check whether the cracks produced by the random walk process are realistic and whether the similarities of cracks can be determined by the algorithm. For this, we produced simple cracks on a two-dimensional model, as shown in Fig. 4(a). Two cracks meet each other to form a Y-shaped crack. These cracks were produced by the random walk algorithm with 130-150 steps starting from the initial point in the middle of the rectangular domain. One of the cracks ended at the edge and the other ended when it met the previously generated one. Fig. 4(b) shows changes made from the last 50 steps, where two cracks do not meet and both end at the edge. Figs. 4(c) and (d) show changes made from the last 100 steps and 150 steps, respectively. In Fig. 4(c), two cracks again form a Y-shaped crack and the two cracks in Fig. 4(d) do not meet each other. However, it is not straightforward to quantify how much they are similar, and therefore we need a quantitative assessment method for determining their similarities.
For describing similarities of images, there are a few quantities, and among these, the “cosine similarity” quantity is one of the simplest quantities for comparing two vector images. The image data for the cracks in this work were composed of values of 0 or 255 for all pixels and were considered as the vector images to be compared. The cosine similarity factor is defined as follows:
Here, |A| and |B| are the respective sizes of each image vector and A·B is the dot product of the two image vectors. Each pixel of the vector images of A and B is defined as Uij and Vij, respectively. Following the definition of the two vector images, we calculated the cosine similarity factor for the simple virtual crack images described in Fig. 4. For the calculations, one of two vector images was the original one shown in Fig. 4(a) and the other was the image made from the last step changes, as shown in Figs. 4(b), (c), and (d).
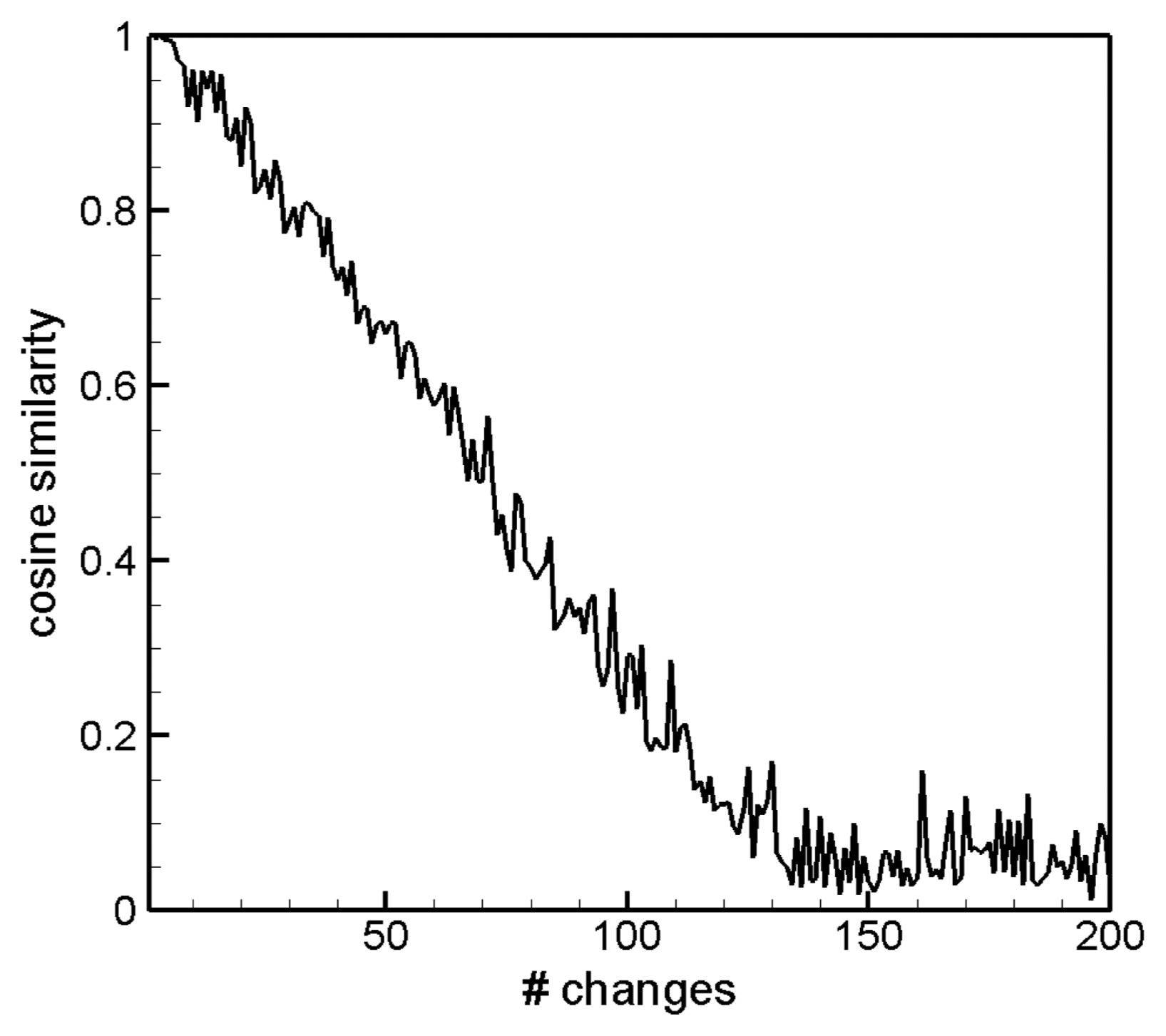
Figure 5 shows the cosine similarity factor of the images shown in Fig. 4. The horizontal axis represents the number of last steps of the change from the original image and the vertical axis represents the calculated value of the cosine similarity factor according to Eq. (1). The value 1 means that the two images are the same and the value 0 means that the images are completely different. As the number of the last steps of the changes increases, the value of cosine similarity decreases downward from 1. The change is nearly linear, and it is shown to approach 0 at step changes of around 130-150. After that, the value continually fluctuates, which is thought to be due to the accidental coincidence of the images during the additional changes after 150 steps. Although the cosine similarity factor is limited to assessing all possible similarities such as translational or rotational variations of the images, it can be still considered a simple and clear way to determine the similarities of virtual cracks generated by the controllable algorithm used in the current study.
5. Conclusions
In this study, we used a mathematical algorithm to generate big data sets for the virtual image patterns of cracks on the surfaces of ceramic products. This stochastic algorithm based on the random walk process was demonstrated to generate realistic images by imposing some constraints, such as uniform step length and limited direction changes. The uncertainty of the virtual data, even under the same process conditions, was shown to be controlled by limiting the maximum variations. Because the optimization by machine learning was performed by the stochastic approach rather than by the deterministic approach, we considered it reasonable to utilize the stochastic approach in the generation of virtual data. Besides these constraints, additional constraints were imposed to mimic the production of ceramics cracks by the various thermomechanical forming processes. For example, crack propagation was finished when it reached an edge of the domain or met other cracks already generated. A variety of different crack patterns could be generated by varying some controlling parameters. By using this algorithm, we generated a large number of vision data sets, so that machine learning could be applied to the generated big data sets to determine optimal conditions on ceramics manufacturing processes, which is the next topic to be addressed in this type of data-based optimization scheme.
Here, we also discuss the validity of the pattern-generation algorithm by checking the similarity of the generated images. The calculated results of the cosine similarity factor according to the step changes presented a reliable relationship between the coincidence of the random walk steps and the similarity of the crack images. It is suggested many different types of geometric parameters (width, depth, and curvature of cracks) can be used to improve the quality control of the realistic images. One example would be another stochastic mathematical model such as fractals. Also, a deterministic Voronoi tessellation model could be introduced to depict various grain-based crack patterns of polycrystalline ceramics such as intergranular, intragranular, and transgranular crack propagations.5) Many other realistic cracks such as those caused by thickness, impurities, or void defects in the ceramics manufacturing process will be addressed in the future.