AbstractMore than two decades of world-wide research efforts have resulted in several classes of potentially important materials. Among them are incipient piezoelectrics, which are especially useful for actuator applications. However, relatively large electric fields are required for activating the large incipient electromechanical strains. So far, many attempts have been made to reduce the required electric field by intentionally inhomogenizing the electric field distribution in the microstructure through core-shell and composite approaches. Here, we show that electric field concentration can be realized simply by adjusting electrode patterns. We have investigated the effect of electrode patterning on the incipient electromechanical strain properties of an exemplarily chosen lead-free relaxor system, revealing that electrode patterning does have a significant role on the strain properties of the given lead-free relaxor system. We believe that this approach would make a new strategy for ones to consider bringing the functional properties of electroceramics beyond their conventional limit.
1. IntroductionDeveloping high-performance lead-free piezoelectrics, an alternative to the market dominated by lead-based piezoelectrics, has been of great interest to the piezoelectric community for more than two decades in response to stricter environmental regulations.1,2) It could be said that two potentially noteworthy outcomes from the more than twenty years of research are the discoveries of the morphotropic phase boundary between rhombohedral and tetragonal symmetry in potassium-sodium niobite (KNN)3) that appears to compete with PZT’s4) and incipient piezostrains in bismuth-based relaxor ferroelectrics, the strain levels of which are almost two times larger than those of typical piezoceramics.5,6) The former is in steady development in the community, but the latter still needs further breakthroughs due to the relatively large electric field level required for activating the aforementioned large strain behavior. Therefore, we focus our discussion only on how to further improve the incipient piezostrains in lead-free relaxor ferroelectrics.
Incipient piezoelectricity was first named in accordance with its phenomenology, namely, the piezoelectricity develops out of a macroscopic paraelectricity beyond a certain electric field level.5) The need for this new naming was justified by the widespread misconception that the presence of so-called a double or pinched polarization hysteresis loop should be a sufficient condition for the antiferroelectricity, although it is merely one necessary condition. In fact, the constriction in the polarization hysteresis loop simply reflects that the system of a concern is a macroscopically paraelectric state in the absence of external electric field, although the state can be transformed into a ferroelectric state by the application of external electric field. In other words, the ferroelectricity in a given material system is only stable upon the application of a certain electric field level, which could be the case for relaxor ferroelectrics, normal ferroelectrics slightly above their Curie point, antiferroelectrics, and other materials.
Relaxor ferroelectrics are of importance among all the known incipient piezoceramics from the practical point of view. Antiferroelectric materials are mechanically unstable due to a significant reversible volume change during each driving cycle and normal ferroelectrics slightly above their Curie point suffer from highly limited temperature range for their use. In contrast, the incipient piezoelectricity in relaxor ferroelectrics emerges if they are above a so-called freezing temperature and persists up to fairly elevated temperatures due to the relatively temperature insensitive electrostrictive coefficient. In addition, the large strain comes from a repetitive poling process during each cycle so that it is free of fatigue.7,8) As recently revealed, relaxor-based incipient piezoceramics are expected to be thermally stable against self-heating due to the presence of electrocaloric cooling at each cycle.9)
Thanks to those results, a number of studies have been performed to make the incipient piezostrains in lead-free relaxor ferroelectrics practically viable, since their mechanism was clearly revealed in 2009.10) Early-stage studies had focused on adjusting the freezing temperature, above which the incipient piezostrains emerge, in various systems. 11-16) However, all the developed systems suffer from an excessively large activating electric field (ER-F: electric field required for relaxor-to-ferroelectric phase transformation - the rationale for the terminology can be found in some works17,18) that was in the way of practical versatility, although most compositions of a potential interest had been thoroughly scanned). The record for the minimum ER-F was reported on a (Bi1/2Na1/2)TiO3-SrTiO3 (BNT-ST) solid-solution system at about 2.3 kV/mm.19) Note that considering the maximum driving field for actuators is 2 kV/mm1, the ER-F needs positioning near 1 kV/mm for stable and reproducible cycling.22)
The first breakthrough in the ER-F reduction was reported on a core-shell structured alkaline niobite system in 2012.23) When a KNN-based system was further modified by the addition of CaZrO3, the strain reached up to ~ 0.4% at 4 kV/mm (~ 1,000 pm/V) with ER-F less than 0.5 kV/mm. This core-shell approach was readily accepted by the community as an ‘ultimate’ solution to the ER-F reduction, because the externally applied electric field should be concentrated on the ferroelectric core with a lower dielectric permittivity.24) Unfortunately, however, a similar effect has not been reported afterwards, which has been attributed to poor reproducibility.
It was not long before a 0-3 composite concept was proposed as an alternative to the core-shell approach.25,26) The idea behind the so-called 0-3 composite approach was quite simple in that it mimicked the core-shell approach by adding a ferroelectric composition as a ‘0’ component into a relaxor matrix as a ‘3’ component. Although the working principle was the same as that of core-shell structured systems, it has been considered by far easier in practice and more reliable in reproduction than the core-shell approach. This is why this 0-3 composite approach is still intensively studied.27-29) Although the 0-3 composite approach may be conceptually correct, the effect does not seem to be as significant in reducing EF-R as formally expected.
The previous attempts all considered inhomogenizing the electric field distribution in a way to let a certain region of the system be exposed to more intensified electric field than the applied field. Given that the concentration of electric field matters, it can naturally be expected that a patterned electrode, like a lightning rod, could yield the same effect. Therefore, we first devised five different types of patterns to see which electrode shape the best effect on the field concentration has, based on the premise that electric field tends to concentrate on conducting edges. It is a matter of course that the higher the concentration is, the better, but too much concentration would lead to an electrical breakdown. Therefore, we also adjusted the inter-electrode distance at three distinct levels to find an optimized patterning scheme. A total of fifteen patterns were tested in the current investigation as shown in Fig. 1 applied to one of the well-known lead-free relaxor systems, 0.97Bi1/2(Na0.78K0.22)1/2TiO3-0.03Bi-AlO3 (BNKT-BA).30) As will be shown and discussed, electrode patterning does have a positive effect on enhancing incipient piezostrains, although there is ample room for further improvement.
2. Experimental ProcedureBi2O3 (99.9% Kojundo), Na2CO3 (99.0%, Sigma-Aldich), K2CO3 (99.0%, Sigma-Aldrich), TiO2 (99.9%, Kojundo), BaCO3 (99.95%, Kojundo), and Al2O3 (99.9%, Kojundo) were weighed to the intended stoichiometric composition of 0.97Bi1/2(Na0.78K0.22)1/2TiO3-0.03BiAlO3 (BNKT-BA). Then, they were mixed and ball-milled with YSZ milling balls for 24 h. The milled powders were dried, and then calcined at 800°C for 2 h. To prepare slurry for the tape casting process, a solvent was prepared by mixing 60 vol% toluene (99.5%, Daejung Chemical & Metals Co., Ltd, Korea) with 40 vol% ethanol (99.5%, Daejung Chemical & Metals Co., Ltd, Korea). Then, polyvinyl butyral (Butvar® B-98, Solutia Inc., USA), dibutyl phthalate (94%, Daejung Chemical & Metals Co., Ltd, Korea), and BYK-111 (BYK Chemical, Germany) were added to the slurry as a binder, a plasticizer, and a dispersant, respectively. The slurry was ball-milled for 24 h. As-milled slurry was tape-casted with the uniform thickness of 30 μm. The patterns for electric field concentration were printed on green sheets with a Ag-Pd paste. The green sheets were stacked and then pressed at 60°C under uniaxial pressure of 100 MPa for 30 s. Each sheet was laminated to the thickness of 0.9 mm and blade-cut in accordance with the guidelines. The processed samples were heat-treated in air at 650°C for 2 h to remove organic matter, followed by sintering in air at 1150°C for 2 h. After sintering, Ag electrodes were painted on both sides of the sample surfaces.
3. Results and Discussion
Figure 2(a) schematically illustrates a step-by-step procedure for the fabrication of lead-free BNKT-BA ceramics intended for electric field concentration. To realize the 3-dimensional electrode patterns, each field-concentration type electrode was screen-printed on top of the as-prepared green sheets and stacked in parallel. The thickness of each layer between electrode patterns was 200 μm after sintering as shown in Fig. 2 (b). Each pattern was connected by external electrodes screen-printed on flank surfaces so that the tip of intended field-concentrating electrode pattern points along the external field direction. An image of each material after sintering at 1150°C for 2 h is presented in Fig. 2(c). The details of the realized patterns viewed through an optical microscope are seen in Fig. 2(d). The thickness of specimens was determined at 1.26 mm and the distance between electrode patterns 0.64 mm after sintering. The values of interval1, interval2, and interval3 were 0.38, 0.63, and 1.46 mm, respectively.
Figure 3 (a) and (b) depicts the polarization and strain hysteresis loop of BNKT-BA. The absence of negative strain strongly supports that BNKT-BA is an incipient piezoceramic. Fig. 3 (c) shows x-ray diffraction patterns and microstructure analysis that reveal that the currently fabricated material has single perovskite structure without secondary phases and high relative density of 98%. The quality of the sample is also guaranteed by the high dielectric breakdown strength, which is well beyond 10 kV/mm. This implies that the chosen BNKT-BA is highly suitable for the current experimental purpose in that materials are supposed to be exposed to a locally generated excessively large electric field.
To estimate the effect of electrode patterning on electric field concentration, a finite element method using a commercial software (QuickField™ ver. 6.3) was utilized to monitor the changes in the electric field distribution as functions of electrode type and interval, as presented in Fig. 4. The applied electric field was set at 1 kV/mm. All patterned electrodes, regardless of their detailed shape profile, impact the field concentration to a degree. We see that the equipotential points stem from the pattern edges and shift in position due to interactions with those from nearby patterns. The degree of interference increases with decreasing inter-pattern distance, leading to a weakening of the intended electric field concentration. For example, one sees that the distribution profile of equipotential lines shown in the (pattern 1, interval 1) case, is quite similar to that of the pattern-less case. This means that once the inter-pattern distance is set below a certain limit, one may expect a sample response typical of higher electric fields in the pattern-less case due not to an electric-field concentration but to the reduction in the active layer. On the contrary, increasing inter-pattern distance, promotes electric-field concentration. However, this leads to the decrease in the pattern density so that active region under the influence of concentrated electric field decreases and overall functional properties converge to those of the pattern-less case. Although the overall trends are consistent for all patterns, it is clearly seen that the detailed effect depends on the shape profile. The sharper the front edge, the higher the level of concentration. For example, patterns 3 and 4 are less susceptible to the inter-pattern distance than patterns 1 and 2, as naturally expected from the shape characteristic. Unexpectedly, pattern 5 was less effective in concentrating the electric field possibly due to the lack of a vertical component in the electric field that prevents the electric field from being concentrated at the tip of the pattern.
Figure 5 is a summary of unipolar strain properties of patterned samples in comparison to the reference sample with a pattern-less electrode up to 5 kV/mm. The larger the inter-pattern distance, the higher the field concentration; thus, chances for dielectric breakdown increase with larger inter-pattern distance. In the case of interval 1 where all the samples survived up to the maximum electric field of 5 kV/mm, the strain properties are evidently enhanced in patterns 3 and 4, while the concentration effect is rather insignificant in patterns 1, 2, and 5. The ineffectiveness in patterns 1 and 2 for the given inter-pattern distance may be due to a significant interference that leads to the reduction in the active region, as predicted by the simulation. Nevertheless, as the inter-pattern distance increases, the expected field concentration is realized, leading to a further enhancement in the strain properties. However, the result for pattern 5 should be due to an undesirable pattern design.
It is seen that the degree of displacement decreases while the saturation behavior starts with the increase in inter-pattern distance in the case of pattern 3. It is noted that pattern 3 consists of a triangular shape that could mitigate the inter-pattern interferences even when the pattern-to-pattern distance is quite small. In fact, pattern 3 already exhibits as high strains for the shortest inter-pattern distance as patterns 1 and 2 with a reduced active layer, that is, the actual electric field applied to the active region is higher than the external field. Nevertheless, the strain tends to decrease with increasing inter-pattern distance. We believe that this is because the concentration effect is more dominated by the decrease in the number density of field concentrators than the strengthened field concentration due to the weakened inter-pattern interferences. In the meantime, pattern 4 also exhibits a similar tendency on the effect of inter-pattern distance as pattern 3. Nevertheless, it is seen that the strain response of pattern 4 does not saturate as it does with patterns 1 and 2 with increasing inter-pattern distance. This implies that pattern 3 is still better in concentrating the electric field. Finally, pattern 5 appears to be the best in electric field concentration, although the effect is largely mitigated due to the inter-pattern interference as expected from simulation. In addition, even adjusting the inter-pattern distance turns out to be ineffective due to an early dielectric breakdown from an overloaded electric field concentration.
As explained earlier, the driving electric field level in this study was set at 5 kV/mm, because the typical electric field level for activating and saturating incipient piezostrains in the known lead-free piezoceramics is fairly large at above 5 kV/mm. However, the apparent effectiveness of the current approach with electrode patterning prevents a proper comparison from being made due to dielectric breakdown. Additionally, the typical driving electric field for actuator applications is much less than 5 kV/mm as discussed earlier in the introduction. Therefore, we chose 3 kV/mm as a driving field to make a proper comparison for the strain responses of each case.
Figure 6 compares the strain responses of each case up to 3 kV/mm. Unlike the high field exposure, no apparent change is noted as a function of the field level and inter-pattern distance except for pattern 3 with interval 3, although the effect is evident for all cases with the enhancement of about 33 ~ 55%. In comparison to the pattern-less case, the strain response at 3 kV/mm is enhanced by 140%, and the strain level of 0.03% at 3 kV/mm for the pattern-less case already achieved at 2 kV/mm. A summary of the current investigation with respect to the key parameter inter-pattern distance is presented in Fig. 7.
4. ConclusionsA new approach to activating incipient piezostrains at the lowest electric field as possible was investigated. We demonstrated that electric fields, which are higher than the externally applied fields, can be successfully induced simply by introducing 3-dimensional patterns. A special emphasis was made on the effect of the shape of patterns and inter-pattern distances on the strain level. We noted that the inter-pattern distance is the most important parameter, and there should be an optimum inter-pattern distance to maximize the strain properties by electric field concentration. This is not only because the shorter the inter-pattern distance is, the less effective the concentration of electric field becomes due to an increasing inter-pattern interference, but also because the strain enhancement assisted by electric field concentration became less effective owing to the reduction in the pattern density. The inter-pattern interference was found to depend heavily on the shape of the electrode pattern only when the inter-pattern distance was short enough for nearby field contours to interfere with each other. Within the framework of this study, a triangular shaped electrode with the largest possible inter-pattern distance showed the best strain properties at a relatively low electric field of 3 kV/mm.
AcknowledgmentsThis work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MEST) (No. NRF-2018R1D1A1B07051176).
NotesAlthough there is no strict rule on the maximum driving field for actuators, the choice of the driving field is commonly made by the minimum required electromechanical strain values, typically 0.1 ~ 0.15%. The piezoelectric actuator market is mostly dominated by PZT-based ceramics, where 1 ~ 2 kV/mm is typically required for achieving such strain level. In addition, more than 2 kV/mm usually induces a dielectric breakdown through the air, the prevention of which complicates the actuator configuration. 20,21) Fig. 2Schematic diagram of (a) processing and images of specimens (b) top view of specimen in the inspection step, (c) specimens after painting top and bottom electrodes and (d) optical microscope image of patterns in each condition. 
Fig. 3Ferroelectric and piezoelectric properties of BNKT-BA; (a) polarization and (b) strain hysteresis loop. (c) X-ray diffraction pattern and microstructure of BNKT. 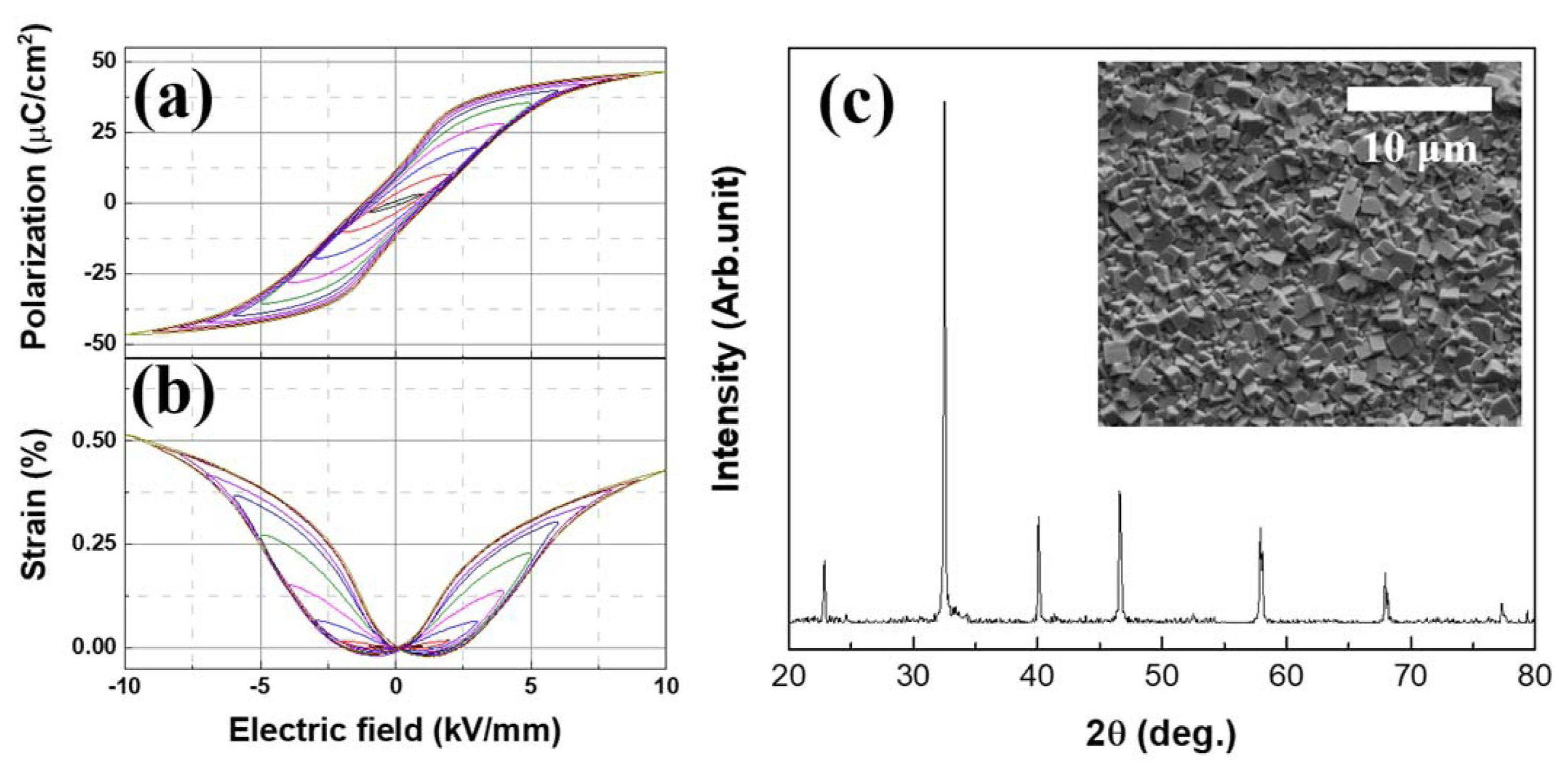
REFERENCES1. C-H. Hong, H-P. Kim, B-Y. Choi, H-S. Han, JS. Son, CW. Ahn, and W. Jo, “Lead-Free Piezoceramics - Where to Move on?,” J Materiomics, 2 [1] 1-24 (2016).
2. H-P. Kim, CW. Ahn, Y. Hwang, H-Y. Lee, and W. Jo, “Strategies of a Potential Importance, Making Lead-Free Piezoceramics Truly Alternative to PZTs,” J Korean Ceram Soc, 54 [2] 86-95 (2017).
3. T-G. Lee, and S. Nahm, “Review of Sintering Technologies, Structural Characteristics, and Piezoelectric Properties of NKN-Based Lead-Free Ceramics,” Trans Electr Electron Mater, 20 [5] 385-402 (2019).
4. J-F. Li, K. Wang, F-Y. Zhu, L-Q. Cheng, F-Z. Yao, and DJ. Green, “(K, Na)NbO3-Based Lead-Free Piezoceramics: Fundamental Aspects, Processing Technologies, and Remaining Challenges,” J Am Ceram Soc, 96 [12] 3677-96 (2013).
5. W. Jo, R. Dittmer, M. Acosta, J. Zang, C. Groh, E. Sapper, K. Wang, and J. Rödel, “Giant Electric-Field-Induced Strains in Lead-Free Ceramics for Actuator Applications - Status and Perspective,” J Electroceram, 29 [1] 71-93 (2012).
6. CW. Ahn, C-H. Hong, B-Y. Choi, H-P. Kim, H-S. Han, Y. Hwang, W. Jo, K. Wang, J-F. Li, J-S. Lee, and IW. Kim, “A Brief Review on Relaxor Ferroelectrics and Selected Issues in Lead-Free Relaxors,” J Korean Phys Soc, 68 [12] 1481-94 (2016).
7. Z. Luo, J. Glaum, T. Granzow, W. Jo, R. Dittmer, M. Hoffman, and J. Rödel, “Bipolar and Unipolar Fatigue of Ferroelectric BNT-Based Lead-Free Piezoceramics,” J Am Ceram Soc, 94 [2] 529-35 (2011).
8. Z. Luo, T. Granzow, J. Glaum, W. Jo, J. Rödel, and M. Hoffman, “Effect of Ferroelectric Long-Range Order on the Unipolar and Bipolar Electric Fatigue in Bi1/2Na1/2TiO3-Based Lead-Free Piezoceramics,” J Am Ceram Soc, 94 [11] 3927-33 (2011).
9. C-H. Hong, H. Guo, X. Tan, JE. Daniels, and W. Jo, “Polarization Reversal Via a Transient Relaxor State in Nonergodic Relaxors near Freezing Temperature,” J Materiomics, online published. PMID: 10.1016/j.jmat.2019.06.00410.1016/j.jmat.2019.06.004.
10. W. Jo, T. Granzow, E. Aulbach, J. Rödel, and D. Damjanovic, “Origin of the Large Strain Response in (K0.5Na0.5)NbO3-Modified (Bi0.5Na0.5)TiO3-BaTiO3 Lead-Free Piezoceramics,” J Appl Phys, 105 [9] 094102(2009).
11. H-S. Han, W. Jo, J-K. Kang, C-W. Ahn, I. Won Kim, K-K. Ahn, and J-S. Lee, “Incipient Piezoelectrics and Electrostriction Behavior in Sn-Doped Bi1/2(Na0.82K0.18)1/2TiO3 Lead-Free Ceramics,” J Appl Phys, 113 [15] 154102(2013).
12. CH. Lee, HS. Han, TA. Duong, TH. Dinh, CW. Ahn, and JS. Lee, “Stabilization of the Relaxor Phase by Adding CuO in Lead-Free (Bi1/2Na1/2)TiO3-SrTiO3-BiFeO3 Ceramics,” Ceram Int, 43 [14] 11071-77 (2017).
13. VDN. Tran, H-S. Han, C-H. Yoon, J-S. Lee, W. Jo, and J. Rödel, “Lead-Free Electrostrictive Bismuth Perovskite Ceramics with Thermally Stable Field-Induced Strains,” Mater Lett, 65 [17-18] 2607-9 (2011).
14. G. Wang, Y-H. Hong, HTK. Nguyen, BW. Kim, CW. Ahn, H-S. Han, and J-S. Lee, “High Electromechanical Strain Properties in SrTiO3-Modified Bi1/2Na1/2TiO3-KTaO3 Lead-Free Piezoelectric Ceramics under Low Electric Field,” Sens Actuators, A, 293 1-6 (2019).
15. K. Wang, A. Hussain, W. Jo, J. Rödel, and DD. Viehland, “Temperature-Dependent Properties of (Bi1/2Na1/2)TiO3-(Bi1/2K1/2)TiO3-SrTiO3 Lead-Free Piezoceramics,” J Am Ceram Soc, 95 [7] 2241-47 (2012).
16. HS. Han, IK. Hong, Y-M. Kong, JS. Lee, and W. Jo, “Effect of Nb Doping on the Dielectric and Strain Properties of Lead-free 0.94(Bi1/2Na1/2)TiO3-0.06BaTiO3 Ceramics,” J Korean Ceram Soc, 53 [2] 145-49 (2016).
17. T. Sebastian, I. Sterianou, IM. Reaney, T. Leist, W. Jo, and J. Rödel, “Piezoelectric Activity of (1-x)[0.35Bi(Mg1/2Ti1/2)O3-0.3BiFeO3-0.35BiScO3]-xPbTiO3 Ceramics as a Function of Temperature,” J Electroceram, 28 [2-3] 95-100 (2012).
18. W. Jo, S. Schaab, E. Sapper, LA. Schmitt, H-J. Kleebe, AJ. Bell, and J. Rödel, “On the Phase Identity and Its Thermal Evolution of Lead-Free (Bi1/2Na1/2)TiO3-6mol% BaTiO3
,” J Appl Phys, 110 [7] 074106(2011).
19. Y. Hiruma, Y. Imai, Y. Watanabe, H. Nagata, and T. Takenaka, “Large Electrostrain near the Phase Transition Temperature of (Bi0.5Na0.5)TiO3-SrTiO3 Ferroelectric Ceramics,” Appl Phys Lett, 92 [26] 262904(2008).
20. B. Liu, X. Liu, P. Li, F. Li, B. Shen, and J. Zhai, “Improving Piezoelectric Properties by Controlling Phase Structure and Crystal Orientation,” RSC Adv, 7 [66] 41788-95 (2017).
21. S. Gebhardt, D. Ernst, B. Bramlage, O. Pabst, and A. Oberdorster, “Micro-Position Stages for Adaptive Optics Based on Piezoelectric Thick Film Actuators,” J Ceram Sci Technol, 06 [04] 285-90 (2015).
22. C-H. Hong, H-S. Han, J-S. Lee, K. Wang, F-Z. Yao, J-F. Li, J-H. Gwon, NV. Quyet, J-K. Jung, and W. Jo, “Ring-Type Rotary Ultrasonic Motor Using Lead-Free Ceramics,” J Sens Sci Technol, 24 [4] 228-31 (2015).
23. S-Y. Choi, S-J. Jeong, D-S. Lee, M-S. Kim, J-S. Lee, JH. Cho, BI. Kim, and Y. Ikuhara, “Gigantic Electrostrain in Duplex Structured Alkaline Niobates,” Chem Mater, 24 [17] 3363-69 (2012).
24. C. Groh, DJ. Franzbach, W. Jo, KG. Webber, J. Kling, LA. Schmitt, H-J. Kleebe, S-J. Jeong, J-S. Lee, and J. Rödel, “Relaxor/Ferroelectric Composites: A Solution in the Quest for Practically Viable Lead-Free Incipient Piezoceramics,” Adv Funct Mater, 24 [3] 356-62 (2014).
25. DS. Lee, DH. Lim, MS. Kim, KH. Kim, and SJ. Jeong, “Electric Field-Induced Deformation Behavior in Mixed Bi0.5Na0.5TiO3 and Bi0.5(Na0.75K0.25)0.5TiO3-BiAlO3
,” Appl Phys Lett, 99 [6] 062906(2011).
26. DS. Lee, S. Jong Jeong, M. Soo Kim, and J. Hyuk Koh, “Electric Field Induced Polarization and Strain of Bi-Based Ceramic Composites,” J Appl Phys, 112 [12] 124109(2012).
27. P. Fan, Y. Zhang, Y. Zhu, W. Ma, K. Liu, X. He, MA. Marwat, B. Xie, M. Li, and H. Zhang, “Large Strain under Low Driving Field in Lead-Free Relaxor/Ferroelectric Composite Ceramics,” J Am Ceram Soc, 102 [7] 4113-26 (2019).
28. MA. Qaiser, A. Hussain, J. Zhang, Y. Wang, S. Zhang, L. Chen, and G. Yuan, “0-3 Type Bi3TaTiO9:40wt%BiFeO3 Composite with Improved High-Temperature Piezoelectric Properties,” J Alloys Compd, 740 1-6 (2018).
|
|
|||||||||||||||||||||||||||||||||||