1. Introduction
Alumina (Al2O3) is an abundant and relatively inexpensive ceramic material that has unique physical and chemical properties. Alumina is one of the oldest types of industrial ceramics that is still prevalent as an industrial material.1) It exhibits two main phases, namely α and γ. The α phase consists of colorless crystals and crystallizes in hexagonal structure, whereas the γ phase is composed of very tiny colourless crystals that exhibit cubic structure and a specific weight of 3.6 g/cm3. The latter phase transforms to the former phase at high temperatures. The stable phase of alumina is corundum, which exhibits a hexagonal close-packed structure composed of oxygen atoms, in which aluminum atoms occupy two-thirds of the octahedral spaces.2,3) Alumina has significant industrial and commercial importance owing to a wide variety of applications in high-strength materials, bioceramics, microelectronics, coatings, abrasive materials, refractory and reinforcing materials, and catalysts.3,4)
In order to enhance the mechanical characteristics of alumina, different additives, including ZrO2,5) MgO,6) Nb2O5,7) and SiC,8) can be added to it. Adding SiC to Al2O3 in the optimum proportion and the mechanisms involving crack deflection, crack bridging, and phase transformation decrease the grain growth rate and increase the grain boundary strength, resulting in the mechanical properties being improved in comparison with those of pure alumina.9,10) This composite can be fabricated through common methods, including pressure-off and cold isostatic press or hot press method. Hot press method generally affords the most favorable properties among all the techniques.9,11) Adding only 5 vol.% nanoSiC to alumina leads to its fracture strength and toughness increasing by 3 and 3.5 times, respectively. Within the sintered and polycrystallized alumina structure, some tensile stress remains at the grain boundaries and in the grains owing to anisotropy in the thermal expansion coefficient and elasticity modulus across different crystallographic directions. In this situation, a crack forms along the grain boundary, with dimensions comparable to that of a grain, owing to the existence of residual stress and defects during the manufacturing process.10,12-14) By sintering alumina at 1500°C, it is quite possible to achieve a density that is close to the theoretical density. However, after adding 5 vol.% nanoSiC particles, condensation of the composite becomes more difficult and it is necessary to increase the sintering temperature up to 1700°C to achieve full density. If the volume fraction of the particles is increased to 10 vol.%, the sintering temperature of the composite should be increased to more than 1750°C to realize full density. Since SiC particles do not have sufficient mobility and do not react with Al2O3 at the sintering temperature, they reduce the mobility of the grain boundaries and, as a result, inhibit the condensation of Al2O3. Hence, after the addition of SiC nanopowders, the sintering temperature should increase.10)
Scientists have figured out that adding low amounts of MgO can lead to increased compressibility of Al2O3, corresponding to the range of the theoretical density. The prevalent theory is that MgO prevents grain growth by decreasing the grain boundary mobility, which is a result of the formation of a solid solution. Another theory includes accelerated condensation of Al2O3 upon adding MgO, in which increases in the network permeation coefficients and a decrease in the surface permeation rate are known to be responsible for this phenomenon.15) In addition, adding MgO to alumina enhances its sintering capability and leads to the fabrication of alumina with a controlled microstructure. 16) In Al2O3-SiC nanocomposites, with regard to the presence of SiC nanoparticles, which reduce the grain boundary mobility, the activated mechanisms that are attributed to the addition of MgO are more complicated, in contrast to those in pure alumina.17)
With respect to the fact that some ceramic characteristics such as ballistic performance depend on a number of parameters, including density, porosity, hardness, fracture toughness, elasticity modulus, sonic velocity, mechanical strength, sintering temperature, and microstructural properties, in this study, nanoSiC powders in volume fractions of 0 to 15 vol.% have been sintered along with micron-sized Al2O3 powders containing 0.08 wt.% nanoMgO at temperatures of 1600, 1650, 1700, and 1750°C. The effects of sintering temperature and different combinations of nanoparticle substances on the mechanical characteristics of the fabricated samples, including the density, flexural strength, elasticity modulus, hardness, and fracture toughness, have been investigated, and phase and microstructural analyses of the samples have been performed.
2. Experimental Procedure
2.1. Materials
The raw materials used for preparing the nanocomposite samples include micronized powder of alumina, silicon carbide nanopowder (nanoSiC), magnesium oxide nanopowder (nanoMgO), isopropanol solution, and argon gas. The alumina powder used had a purity of 99.6% and its chemical composition is as listed in Table 1; its average size was less than 5 μm, with the main phase being γ-Al2O3.
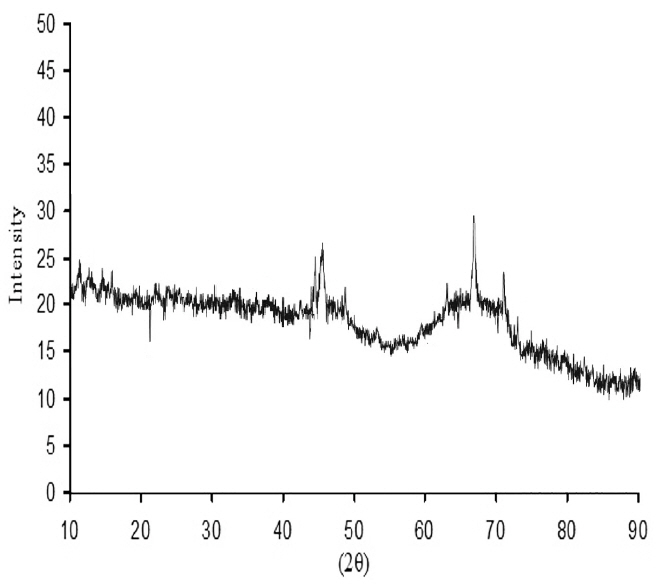
Figure 1 reveals the X-ray diffraction (XRD) pattern of the alumina powder, which indicates the presence of γ-Al2O3 phase.
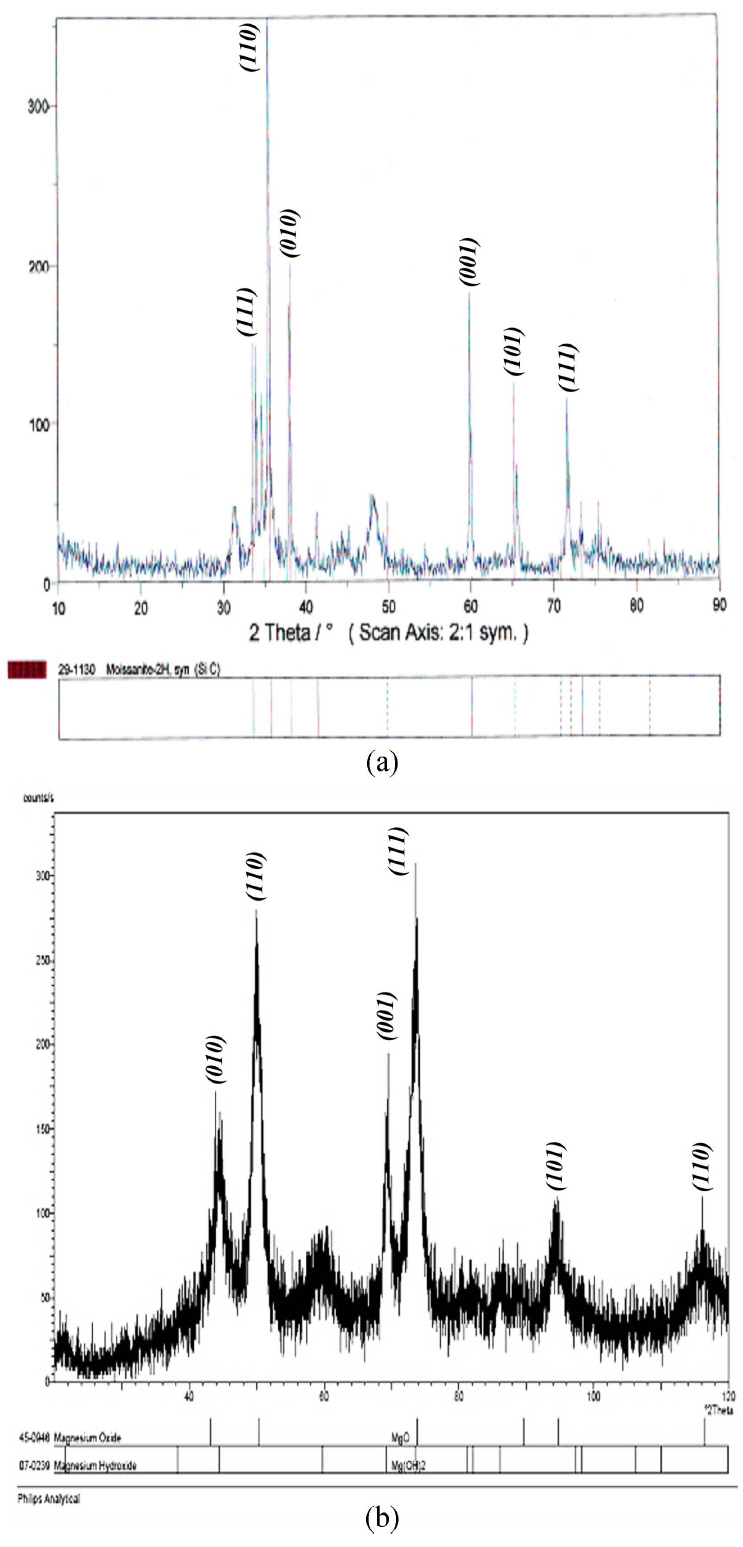
The microstructural images of the alumina, nanoSiC, and nanoMgO powders obtained by SEM or TEM are shown in Fig. 2, which reveals the existence of particles with the maximum size of roughly 5 μm in the Al2O3 powder. The SiC nanopowder used in this experiment contains α-SiC phase with an average size of 70 nm. The MgO nanopowder used was obtained by thermal decomposition of ammonium oxalate and magnesium sulfate with particle sizes less than 100 nm, and is a result of the research work of Ahmadzadeh et al..18) The XRD patterns of nanoSiC and nanoMgO are displayed in Fig. 3.
Isopropanol with the chemical formulation of C3H7OH and purity 99.6% was used in a ball-mill environment. The argon gas employed was 99.99% pure, and the results of its chemical analysis are as follows.
The chamber used for the ball-milling is made of stainless steel, with the inner wall composed of 17 tungsten carbide (WC) balls having the diameter of 17 cm. In order to dry out the samples and expedite the evaporation of alcohol over them, a laboratory drier machine manufactured by Elektro-Warme-Aachen Co. (model FTK) was used. In order to polish the samples, diamond pastes of variety 30, 6, and 1 μm were used. The samples were mounted with a Struers Primopress machine, and Stypex materials were manufactured by Ampco Company at the temperature of 155°C by applying a force of 27 KN on the samples. To determine the flexural strengths of the samples, a five-ton machine manufactured by Zwick Company was used at the loading rate of 0.7 mm/min. To apply Vickers impressions on the samples, the hardness machine UV1 model manufactured by Koopa Company was utilized. To measure and observe the impressions made by the Vickers indenter on the samples, the hardness machine FM-700 model manufactured by Future Tech Company was employed. To study the microstructure of the samples and perform calculations based on the Vickers impressions, a SEM manufactured by Philips Company (model XL30) was used at the voltage of 20 KV and wavelength of λ = 1.54 Å. For phase analysis of the materials, the XRD equipment model 3003TT manufactured by Seifert Company was used.
2.2. Procedure
The samples were fabricated by using hot press method with simultaneous application of heat and pressure on the mixture of primary nanopowders. The value of the nano-MgO was 800 ppm in proportion to the weight of the solid sample, whereas the values of the nanoSiC were 0, 2.5, 5, 7.5, 10, and 15 vol.%. After weighing the primary nanopowders, a suspension of their mixture was prepared in isopropanol and placed inside the ball-mill enclosure for homogenization for 3 h. The ball-to-powder ratio was 14:1. Afterwards, the resulting mixture was placed in an oven at the temperature of 90°C for 24 h. A mass of 330 g of the resulting powder then formed by using a press machine at a pressure of 2 MPa for 30 s. The resulting samples were placed in a hot-press machine for synthesis at the heating rate of 10°C/min in argon atmosphere with a graphite mold at temperatures of 1600, 1650, 1700, and 1750°C by simultaneously applying a pressure of 35 MPa for three hours. Then, the furnace was turned off to allow the samples to lose their heat and cool naturally to the room temperature. By heating the samples at 1000°C inside a heat-treatment furnace for three hours, the graphite attached to the samples in the sintering phase was removed. Meanwhile, thermal etching of the samples was performed for the purpose of examination of their microstructures.
Five pieces of samples were prepared and their densities and porosities measured through Archimedes method based on ASTM B311 standard.19) The theoretical density of the composite sample can be obtained from Eq. (1), in which the alumina density (dA) is equal to 3.986 g/cm3, SiC density (dSiC) is equal to 3.217 g/cm3,20) and MgO density is 3.58 g/cm3.21)
where WA is the weight fraction of the alumina powder, WSiC is the weight fraction of the nanoSiC, and WMgo is the weight fraction of the nanoMgO in the composite.
The exterior volume (V) of the experimental samples can be obtained by Eq. (2) as the difference between the immersion weight and the saturation weight.
Assume that water weighs 1 g. This assumption for water at room temperature would correspond to a volume of 1 cm3 with the approximation of one-thousandths, which can be calculated as the percentage of the open porosity volume with respect to its total volume. The apparent porosity is calculated by Eq. (3).
Water absorption (A) can be quantified as the percentage of the weight of absorbed water relative to the dry sample weight (Eq. (4)):
The apparent density (T) refers to a portion of the sample that is water proof and is obtained by Eq. (5).
The relative fraction of the apparent density of the sample to its theoretical density is calculated according to Eq. (6).
where T is the nominal (apparent) density and dcom. is the theoretical density of the composite. The flexural strength or modulus of rupture (MOR) of the samples was obtained based on ASTM C1161 standard22) by using the three-point method and Eq. (7) with three repetitions of the measurement per sample.
where F is the break force, l is the support span, b is the width of the sample, and d is the thickness of the sample. The elasticity moduli of the samples can be obtained based on ASTM C769 standard23) by considering the changes in sonic velocity in the sample material. In this method, an ultrasonic pulse with the frequency of 4 MHz that is generated by the energy converter machine Echometer1070 manufactured by Karl Deutsch Wuppertal and equipped with DSE Lemo probe, which converts electrical energy to sonic waves, is transmitted through each sample four times and the reflected wave measured. By recording the reversal time and measuring the sample thickness, the sonic velocity in the sample is determined. By using Eq. (8), the elasticity modulus (E) is obtained.23)
where ρ is the density of the sample and ν is the sonic velocity of the sample. The hardness values of the samples were calculated by Vickers method based on ASTM C1327 standard. 24) By applying 49 N (5 kgf) load through a hardness machine for 30 s, seven impressions of the Vickers indenter were created on each sample and, by using Eq. (9), the Vickers hardness (H) was calculated.
where P is the load applied for producing the Vickers impressions and d is the average diameter of the Vickers impressions. The average resulting from the seven measurements of the hardness was reported as the sample hardness. By using Eqs. (10) to (12), the fracture toughness (KIC) values of the samples can be calculated.25-27)
where E is Young’s modulus, Hv is Vickers hardness, P is the load applied for creating the Vickers impressions, tave is the average thickness of the microcracks formed around the indented section, A is the surface area corresponding to the effect of the whole microcracks formed around the indented section of the sample, C is the crack length of the median/radial, and a is one-half of the diameter of the indented section on the sample that is created by the application of the Vickers diamond. The average resulting from the seven measurements was reported as the fracture toughness of the sample.
The surface morphologies of the samples and the dimensions and shapes of the nanoparticles were investigated by SEM in the secondary electron (SE) and back scattered electron (BSE) modes. Furthermore, the grain size of the matrix phase was calculated by using a Philips-FEGC200 transmission electron microscope.
3. Results
3.1. Relative density
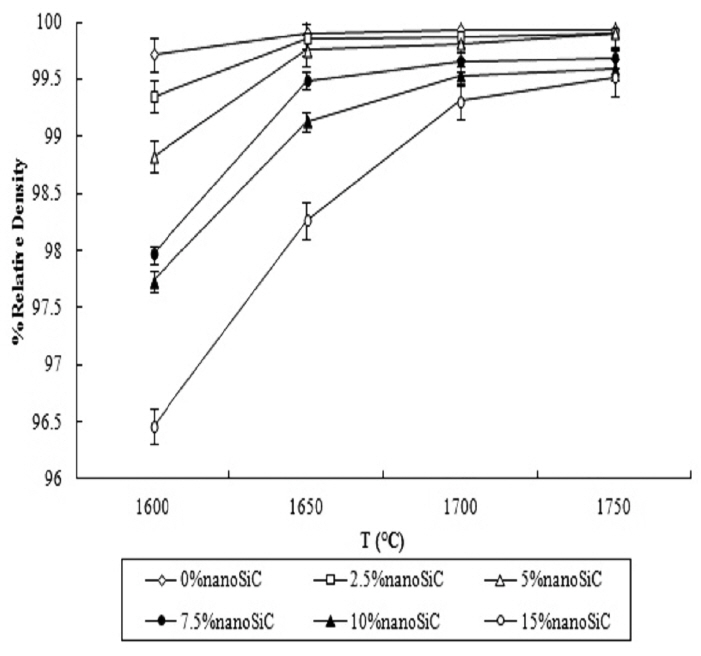
Figure 4 shows the relative densities of the samples as functions of the sintering temperature for different volume fractions of nanoSiC. As observed, with the increase in the sintering temperature for all volume fractions of nanoSiC, the relative density increased. The increase in temperature causes the mobility of the grain boundaries and, as a result, alumina condensation is promoted. Wang et al.10) showed that with the increase in the sintering temperature of an alumina nanocomposite containing 10 vol.% nanoSiC up to 1700°C, a density close to the theoretical density can be possibly realized. The results of this research also verify this finding. The increase in the temperature for different nanoSiC volume fractions eventually leads to an increase in the density up to the theoretical density. On the other hand, addition of SiC nanoparticles decreases the density. It seems that at lower temperatures, this reduction in density has a greater effect due to the lower sintering capacities of the samples. The effect of increased temperature on the increase in the density would be different for different nanoSiC volume fractions, such that it is enormously increased upon increasing the nanoSiC volume fraction in the range of sintering temperatures 1600 to 1700°C. Moreover, at all temperatures, the relative density decreases. Since nanoSiC particles contribute to the immobility of the grain boundaries and prevent Al2O3 condensation, the addition of nanoSiC leads to the relative density being decreased.
In addition, it is revealed that the relative density of the alumina sample containing no nanoSiC additive increases up to 99.9%. The achievement of such a high density can be ascribed to the existence of MgO. It is assumed that MgO forms a solid solution that reduces the volume of grain boundaries. Similarly, excessive grain growth is minimized. On the other hand, the increase in the surface permeability and mobility of the pores causes the porosity of the sample to be reduced. Therefore, the sample density is increased during sintering.16,17,28-30)
3.2. Phase analysis, microstructure, and variations in the grain sizes of samples
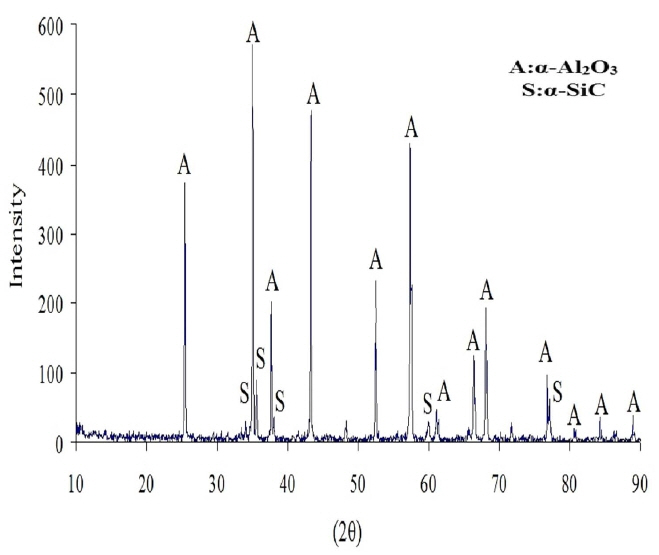
Figure 5 shows the XRD pattern of Al2O3-nanoSiC sample sintered at 1750°C with 15 vol.% nanoSiC, in which the existence of α-Al2O3 and α-SiC without any reaction occurring between them at the experimental temperature and pressure has been illustrated.
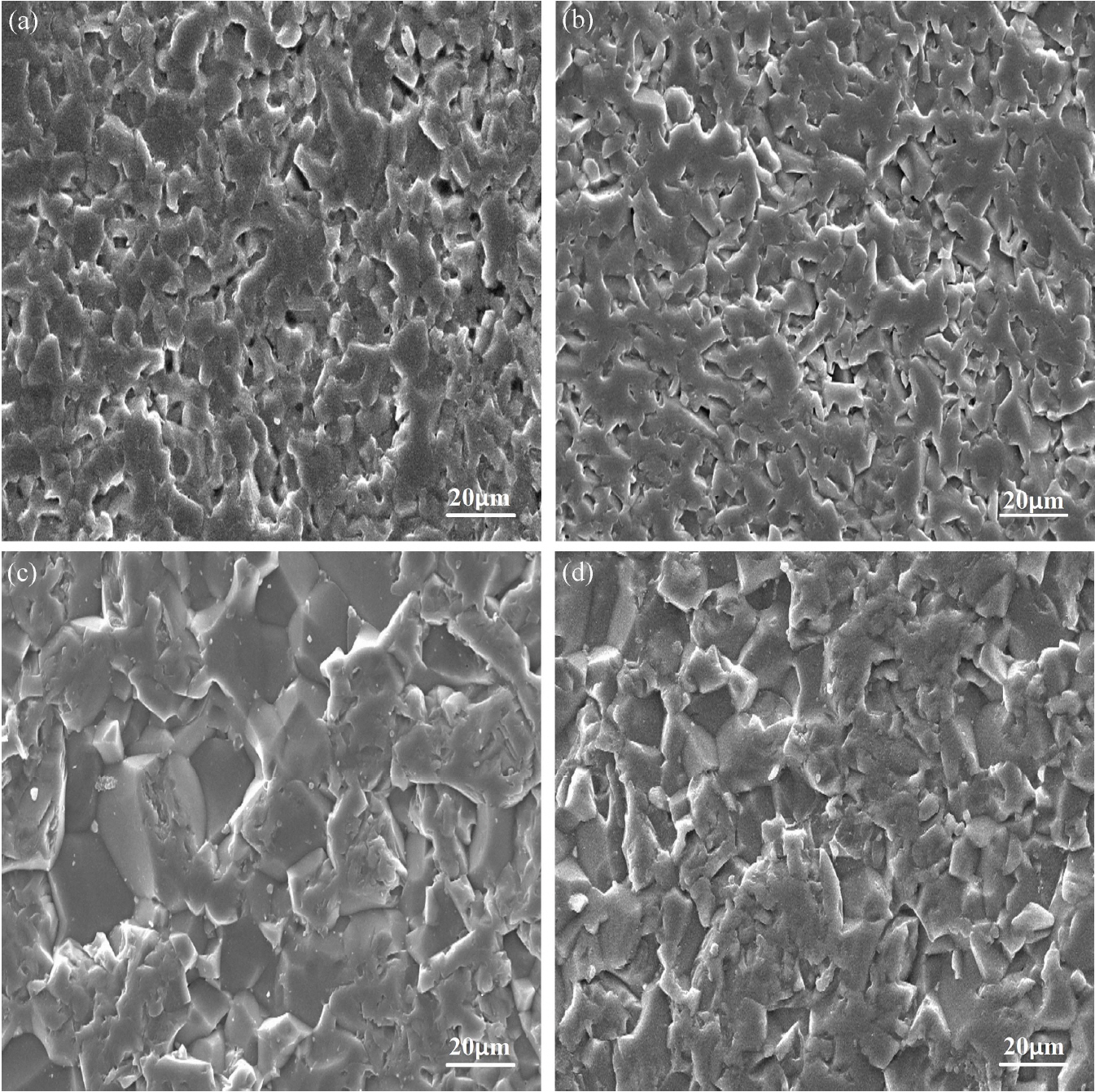
Figure 6 presents the microstructures of some of the sintered samples obtained by SEM at different temperatures. As observed, with the increase in the sintering temperature, the alumina grains become larger; on the other hand, an increase in the volume fraction of nanoSiC prevents extreme growth of the alumina grains. Wang et al.17) proved that monophase Al2O3 grains are large and heterogeneous and that some of the grains grow extraordinarily. However, the addition of nanoSiC particles inhibits the extraordinary growth of the grains and maintains a small grain size. In addition, the grains get homogenized in the composite.
Based on Fig. 6, with the increase in the nanoSiC volume fraction in the samples, the grain size decreases at all the temperatures, which can be attributed to the lack of reaction between the nanoSiC particles and the alumina matrix at the sintering temperatures and to the effect of the nanoSiC particles in reducing the mobility of the grain boundaries.10,31-34) Furthermore, it has been demonstrated that based on Zener model, the secondary phase refrains from the growth of matrix grains, the size of which (G) can be obtained from Eq. (13).17)
where r is the radius of the grains of the secondary phase and f is the volume fraction of the secondary phase. This equation shows that with the increase in the volume fraction of the secondary phase, the grain size of the matrix is decreased. Fig. 7 shows a TEM image of the microstructure of a nonadditive sample that was sintered at 1600°C. Based on the figure, the average size of the sample seed is about 6 μm.
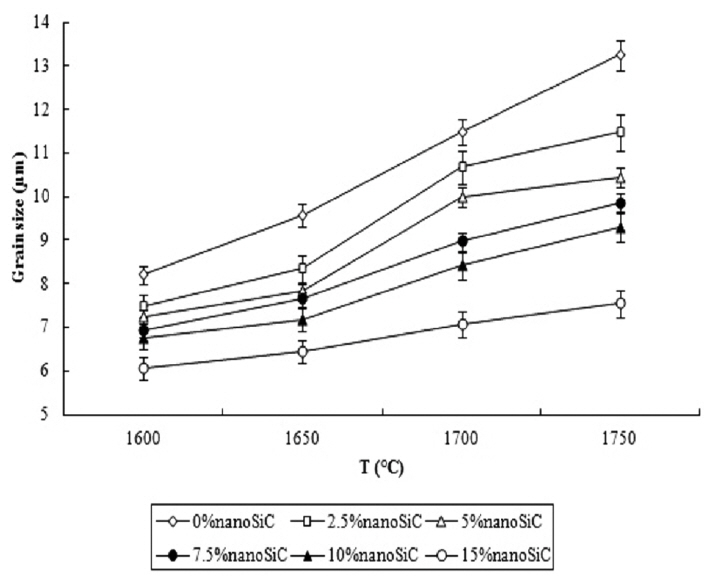
In Fig. 8, the average grain sizes of the samples have been shown as functions of the sintering temperature for different nanoSiC volume fractions. This figure reveals that with the increase in temperature, the grain size increases for all the cases. With the addition of nanoSiC particles, the rate of increase in the grain size is reduced, so that the maximum increase in the grain size is for the nonadditive sample, about 61%, and the minimum value is for the sample containing 15 vol.% nanoSiC, roughly 24%. Moreover, the alumina grain size of the samples increases from the maximum initial size of 5 μm to about 6-14 μm.
Figures 9(a) and 9(b) show the microstructural SEM images of the sample containing 2.5 vol.% nanoSiC and sintered at 1600°C and the sample containing 7.5 vol.% nanoSiC and sintered at 1700°C, respectively, which were obtained by using a BSE detector. As is evident, the nanoSiC particles are located at the grain boundaries and inside the alumina grains. With the increase in the nanoSiC volume fraction, its effect in preventing grain growth does not increase linearly. The reason is that, for example, when the SiC volume fraction is duplicated, a substantial fraction of the particles will occupy the interior of the alumina grains, which implies that the nanoSiC particles existing at the grain boundaries and preventing their growth have not been duplicated. Moreover, owing to the increase in the sintering temperature, the effect of the added nanoSiC particles in inhibiting grain growth will be somewhat decreased.10)
Alumina grain overgrowth often occurs owing to the extremely high energy. Controlling the grain growth in terms of its size and morphology is highly important, as it plays an important role in determining the quality of the produced material; in addition, realizing a high density that is required to stop the growth during sintering is crucial. Therefore, the inhibition of grain growth is utilized as part of the solid solution mechanism in the production of alumina. The important effects of adding MgO include a reduction in the mobility of the grain boundaries, an increase in the surface permeation, and, as a result, an increase in the mobility of the pores, an increase in the condensation with increases in the grain boundaries and network permeation, and reductions in the surface energy and nonuniformity of the grains. Moreover, as the SiC particles do not have enough mobility and do not react with Al2O3 at the sintering temperature, they reduce the mobility of the grain boundaries and, as a result, prevent the Al2O3 condensation. Therefore, after the addition of SiC nanopowder, this issue is addressed by increasing the sintering temperature.
4. Discussion
4.1. Elasticity modulus
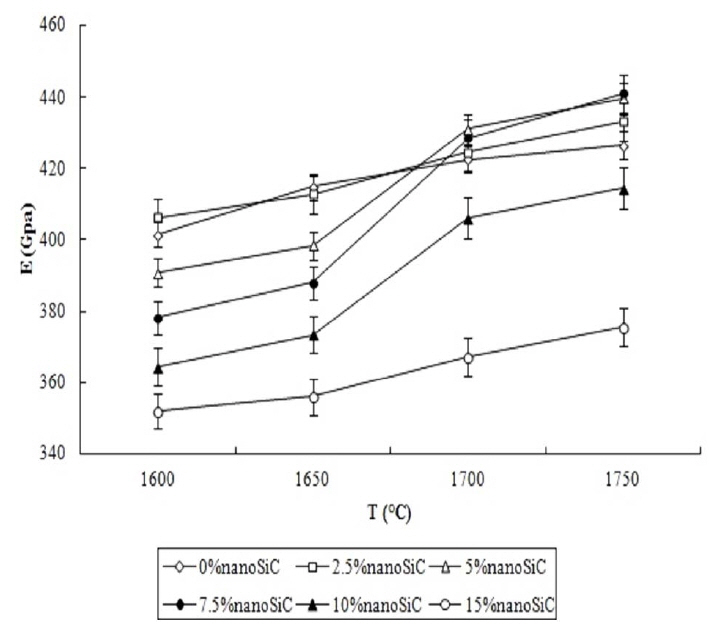
The elasticity moduli of the samples have been shown as functions of the sintering temperature for different volume fractions of nanoSiC in Fig. 10. As seen, with the increase in temperature, the elasticity modulus increases for all the samples, which can be due to the completely sintered particles. With complete sintering, the porosity of samples is reduced and the sonic velocity is increased throughout the sample, which causes the elasticity modulus to be enhanced.31) The elasticity moduli of the sintered samples follow increasing trends up to 7.5 vol.% of nanoSiC at 1700 and 1750°C, before decreasing. The increased elasticity modulus upon adding nanoSiC can be ascribed to the relatively high elasticity modulus of SiC compared to that of Al2O3.31) The elasticity modulus of monocomponent alumina has been reported to be roughly 340-400 GPa in the literature2,32) which suggests that the elasticity moduli of the nonadditive samples, which are in the range 401-426 GPa, exceed that of monocomponent alumina. Anya et al.31) achieved the maximum elasticity modulus of 409.5 GPa for a sample with a relative density of 99.6% that was obtained through pressure-off synthesis and sintering of Al2O3-SiC nanocomposites. Moreover, Moradkhani et al.33) obtained an elasticity modulus of 402 GPa for hot press sintered alumina samples containing 15 vol.% 800 nm SiC particles at 1700°C. The results indicate an increase in the elasticity modulus of the composite.
According to the combination law for a particle (powder) composite with a random phase distribution, the elasticity modulus of the composite can be calculated by using Eq. (14), based on the elasticity modulus of the components.
Where Ei and Vi are the elasticity modulus and volume ratios, respectively, of the components of a composite. Therefore, Eq. (15) is obtained for Al2O3-SiC composite.
where Ecomp is the elasticity modulus of the composite, EA is the elasticity modulus of Al2O3, equal to 380 GPa, and ES is the elasticity modulus of SiC, equal to 414 GPa.34) Therefore, it is expected that with the increase in the amount of SiC, the elasticity modulus of the composite will increase. In contrast, the increase in SiC volume fraction leads to a decreased density and the creation of pores that contributes to a reduction in the sonic velocity in the sample and, hence, the elasticity modulus is decreased.31)
4.2. Hardness
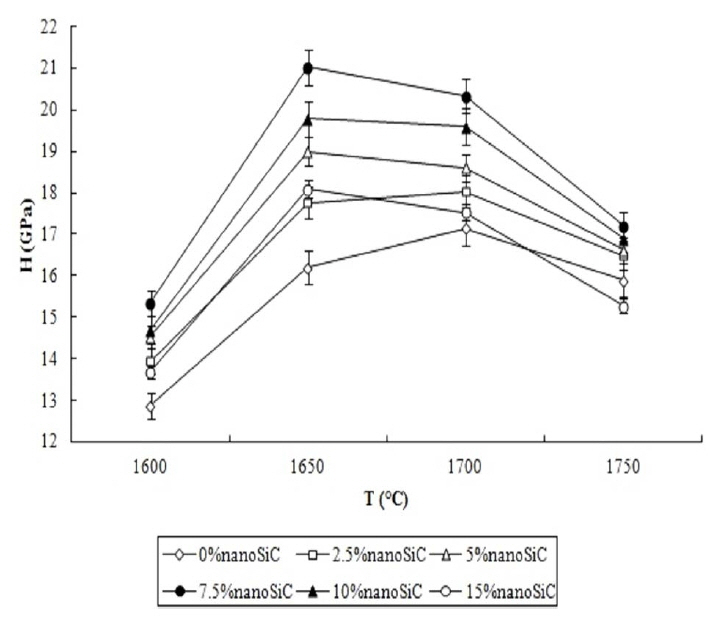
Figure 11 illustrates the Vickers impressions produced on a few samples for the determination of their hardness. In Fig. 12, the hardness values of the samples have been presented in terms of the sintering temperature for different volume fractions of nanoSiC. It is revealed that with the increase in the sintering temperature up to 1650°C, the hardness is increased for all the samples, which can be caused by the completely sintered particles, whereas after that, the hardness decreases owing to grain growth.35,36) The hardness of the alumina sample without nanoSiC added is 12 GPa (which is the least) at 1600°C, which is increased to nearly 17 GPa at 1700°C. The hardness of monocomponent alumina was reported to be about 12-18 GPa.3) In addition, the hardness of the sintered samples increases upon increasing the nanoSiC volume fraction up to 7.5 vol.% at all the temperatures, which can be attributed to the finer grains existing in the structure with the increase in the nanoSiC volume fraction.31) The hardness of Al2O3-SiC nanocomposite containing 20 vol.% 200 nm SiC particles prepared by hot press method at 1740°C reaches 19.7 GPa maximum, which is approved based on the current findings. 12) It seems that with the increase in the nanoSiC volume fraction beyond 10 vol.%, the porosity is increased, while the density is decreased, which cause a reduction in the hardness. On the other hand, agglomeration of the nanoSiC particles increases and their distribution homogeneity in the alumina matrix decreases, and hence, the hardness declines. In addition, with the increase in the nanoSiC volume fraction of the composite, the residual stress resulting from the discrepancy in thermal expansion between SiC? and Al2O3 increases, until it is released, which leads to the formation of microcracks in nanoSiC; as a result, the hardness is reduced.36)
4.3. Fracture toughness
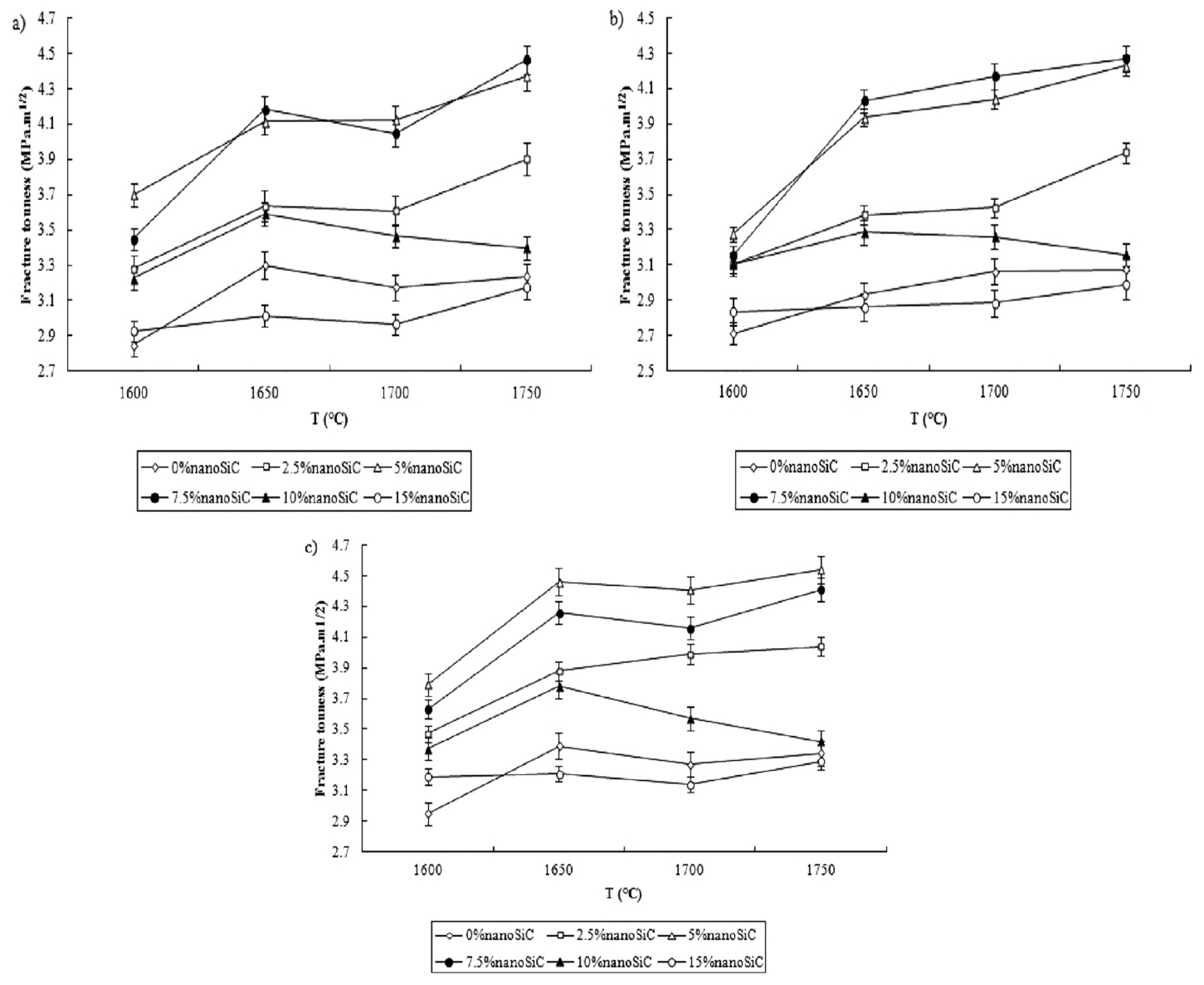
Figure 13 displays the changes in the fracture toughness of the samples resulting from Eqs. (10) to (12) as functions of the sintering temperature. Through careful attention and comparison of the results, it can be learned that the findings from Eq. (10), which have been recently presented and used for a few brittle materials,33,37-40) exhibit a high accuracy. As it turned out from the comparison of the results, the difference between the findings from Eq. (10) and all the other findings is less than 13% for all the cases.
As observed, with the increase in the sintering temperature up to 1650°C, the fracture toughness is increased, owing to the samples being completely sintered. Further increases in temperature lead to minor changes in the fracture toughness of the samples. The reduction in the fracture toughness with the increase in temperature can be ascribed to increased grain size; on the other hand, the increase in the fracture toughness caused by an increase in temperature can be attributed to a reduction in the defects and pores, which are sources of cracks.31,35) The increase in the fracture toughness at 1750°C can be attributed to the formation of combined phases such as mullite (3Al2O3.2SiO2), which results from the reaction of SiO2, available at the SiC particle surfaces, with alumina, and also to the partial formation of the spinel phase MgO. Al2O3 at high temperatures. The resulting phases can be observed at the grain boundaries and pores, and resist crack growth, thus increasing the fracture toughness.11) Moreover, the fracture toughness of the samples is increased by adding nanoSiC up to 5 vol.% and, in some cases, up to 7.5 vol.%. The mechanisms of enhancement in fracture toughness that include crack deflection and microcrack toughening have been proposed for the improvement in the toughness upon increasing the nanoSiC volume fraction.30) Other studies also verify the increase in the fracture toughness of alumina samples, from almost 1.2 to 4.5 MPa.m1/2.33) The fracture toughness of alumina nanocomposites containing SiC additive has been reported to be in the range 2-4.5 MPa.m1/2, which is in agreement with the current findings.2,12)
With the increase in the nanoSiC volume fraction, the agglomeration of the nanoSiC particles is increased and their distribution homogeneity in the alumina matrix is decreased. On the other hand, the residual stress resulting from the discrepancy in thermal expansion between SiC? and Al2O3 is increased, which is eventually released, causing the grain boundaries to get clinched. As a result, with the decrease in the resistance to crack formation, the fracture toughness is also reduced.36,41)
4.4. Flexural strength
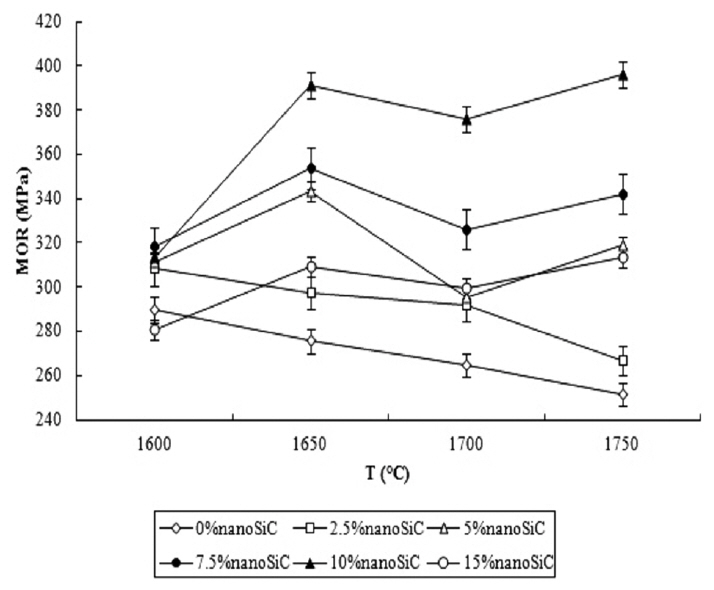
Figure 14 shows the flexural strengths of the samples as functions of the sintering temperature for different nanoSiC volume fractions. As is evident, the flexural strength continuously decreases with the increase in the sintering temperature for the nonadditive sample and the sample with 2.5 vol.% nanoSiC. This can be attributed to the increase in the grain size during the rise in temperature, which decreases the flexural strengths of the samples. In the samples with 5 vol.% or more nanoSiC, the temperature required for complete sintering of the samples is increased, owing to the existence of SiC particles and the high melting temperature of SiC (nearly 2670°C), compared to that of Al2O3 (roughly 2050°C).2) Consequently, the increase in the temperature up to 1650°C contributes to the increase in the sintering capacity of the sample being more than the increase in the grain size. Thus, the flexural strength of the sample is increased.
However, the increase in the sintering temperature to 1700°C results in a notable increase in the grain growth. This increase in the grain growth has a more significant impact on the flexural strength in comparison to the increase in the sintering temperature from 1650 to 1700°C, which causes the strengths to be decreased.35)
In the samples containing more than 2.5 vol.% nanoSiC, the increase in the temperature up to 1750°C leads to an increase in the strength. This can be described by the formation of combined phases such as mullite (3Al2O3·2SiO2), which results from the reaction of SiO2, available at the SiC particle surfaces, with alumina, and also to the partial formation of the spinel phase MgO·Al2O3 at high temperatures. The resulting phases can be observed at the pores and grain boundaries, and resist the crack growth caused by stress, thus increasing the strength.11,41,42) The flexural strengths of the samples increase upon adding nanoSiC up to 10 vol.%. A portion of this increase can be attributed to the finer grains existing in the structure upon the addition of the SiC nanoparticles.36) That is because the nanoSiC particles lack sufficient mobility, and also because they do not react with alumina, which reduce the mobility of the grain boundaries. Therefore, a structure with smaller grain dimensions can be obtained.
It seems that with the increase in the amount of nanoSiC, in addition to increasing the porosity and decreasing the density, the agglomeration of the nanoSiC particles is increased and their distribution homogeneity in the alumina matrix is decreased. Thus, the flexural strength is decreased. On the other hand, with the increase in the nanoSiC volume fraction of the composite, the residual stress resulting from the discrepancy in thermal expansion coefficient between SiC and Al2O3 is increased, until it is released, which produces microcracks in nanoSiC; as a result, the strength is decreased.36) The flexural strength of monocomponent alumina has been reported to be about 270-370 MPa in the literature;3) the current findings reveal higher flexural strengths of monocomponent alumina in some cases. The highest strength is obtained for the sample containing 10 vol.% nanoSiC at the sintering temperature of 1650°C or higher; this reflects the increase in the flexural strength of alumina from 251 MPa in the nonadditive nanoSiC sample to 396 MPa in a sintered sample at 1750°C, which correspond to an increase of 57%.
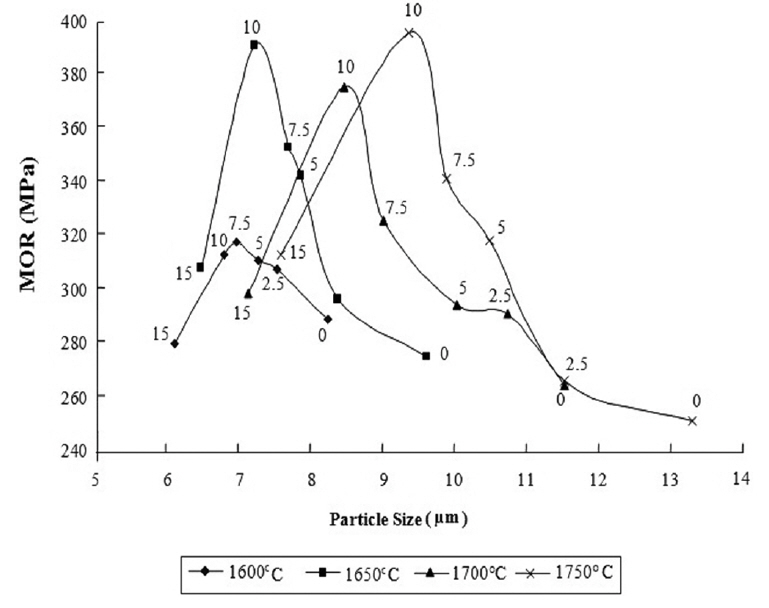
Figure 15 shows the changes in the flexural strengths of the samples as functions of the grain size at different sintering temperatures. As observed, with the decrease in the grain size, the strength is increased. However, in the sample with 15 vol.% nanoSiC, the strength decreases, which can be ascribed to the increase in porosity and release of the residual stress developed inside the grains.36)
Adding SiC particles leads to homogeneity of the structure, in addition to preventing extraordinary growth of the grains and maintaining their dimensions small, which heavily impacts their mechanical properties, including the increase in the flexural strength. On the other side, because the residual stress originating from the discrepancy in the thermal expansion coefficient between SiC and Al2O3, strengthens the grain boundaries, the flexural strength increases.42) The relation between the yield stress (σy) and the grain diameter (d), called Hall-Petch equation, has been expressed in Eq. (16).43)
Here, σ0 is a material constant denoting the initial stress in the dislocation direction and k is an inherent constant of the material. The Hall-Petch equation verifies the increased strength of the material with the decrease in the grain size. The thermal expansion coefficient of alumina in the temperature range 0-1727°C is increased to be roughly 8.58 × 10−6/°C, whereas the thermal expansion coefficient of SiC is nearly 4.70 × 10−6/°C in the temperature range 0-1700°C.42) As a consequence, when cooling a Al2O3/SiC composite sample in a hot press furnace after heat treatment, the Al2O3 particles tend to shrink more than the SiC particles, which produces a compressive stress on the nanoSiC particles present at the grain boundaries, which ultimately increases the resistance of the grain boundaries to slippage. Thus, the strength of a sample is increased upon adding nanoSiC particles. 44)
5. Conclusions
This study investigated the effect of sintering temperature on the mechanical characteristics of alumina-based nanocomposites containing nanoMgO and nanoSiC additives and analyzed their microstructures. The results obtained can be summarized as follow.
With the increase in the sintering temperature, the relative density is increased for all nanoSiC volume fractions, so that the relative density is increased from about 96.5% for 15 vol.% nanoSiC sample sintered at 1600°C to 99.5% for the sample sintered at 1750°C. Furthermore, the relative density of the alumina sample containing nanoMgO without any nanoSiC additive increases to 99.9%, which decreases with the increase in nanoSiC volume fraction at all the sintering temperatures. The realization of such a high density can be ascribed to the existence of MgO.
The XRD pattern of the Al2O3-5 vol.% nanoSiC sample containing α-Al2O3 and α-SiC shows that no considerable reaction takes place between Al2O3 and nanoSiC at the experimental pressure and temperature.
The alumina grain size varies from 6.06 μm for the sample containing 15 vol.% nanoSiC sintered at 1600°C to 13.25 μm for the nonadditive sample sintered at 1750°C. With the decrease in the sintering temperature and increase in the nanoSiC volume fraction, the alumina grain size increases.
The elasticity moduli of the samples are in the range 401- 426 GPa, which follows an increasing trend up to 7.5 vol.% nanoSiC, before decreasing, for the samples sintered at 1700 and 1750°C and containing nanoSiC additive. The increased elasticity modulus upon adding nanoSiC can be ascribed to the relatively high elasticity modulus of SiC compared to that of Al2O3. In contrast, the increase in SiC volume fraction leads to decreased density and formation of pores, which contributes to the reduction in the sonic velocity in the sample and, thus, the elasticity modulus is decreased.
The minimum hardness value of nearly 12 GPa corresponds to the nonadditive alumina sample sintered at 1600°C, and reaches the maximum of 21 GPa upon increasing the sintering temperature to 1650°C and adding 7.5 vol.% nanoSiC, which suggests an increase of 63%. The hardness of the sintered samples is increased by increasing the nanoSiC vol.% up to 7.5 vol.% at all the temperatures, which can be attributed to the finer grains existing in the structure upon increasing the nanoSiC volume fraction.
Upon adding nanoSiC up to 7.5 vol.%, the fracture toughness of the samples is increased; at higher values of nanoSiC addition, the fracture toughness decreases. The increase in the fracture toughness caused by the increase in temperature can be attributed to a reduction in the defects and pores, which are sources of cracks. On the other hand, the reduction in the fracture toughness observed with increasing temperature can be ascribed to the increased grain size. Further, the results obtained from Eq. (10) differ by less than 13% from the results obtained by using other equations pertaining to fracture toughness.
The flexural strengths of the samples sintered at 1750°C increase from 251 MPa for the nonadditive sample to 396 MPa for the sample containing 10 vol.% nanoSiC, which corresponds to an increase of 57%. Moreover, the increase in temperature up to 1650°C contributes to the increase in the sintering capacity of the sample being more than the increase in the grain size. Therefore, the flexural strength of the sample is increased. However, with the increase in temperature up to 1700°C, grain growth leads to a reduction in the flexural strength of the sample.