Kim, Ahn, Hwang, Lee, and Jo: Strategies of A Potential Importance, Making Lead-Free Piezoceramics Truly Alternative to PZTs
Abstract
Active search for lead-free piezoceramics over the last decade has harvested a considerable amount of achievements both in theory and in practice. Few would deny that those achievements are highly beneficial, but agree that this quest of developing the lead-free piezoceramics in replace for PZTs is successfully completed. Nevertheless, few would clearly state where this quest should be directed in our next move. A source of this uncertainty may originate from the fact that it is still not clear how good is good enough to beat PZTs. In this short review, we analyzed the existing literature data to clearly locate the current state of the art of lead-free piezoceramics in comparison to PZT-based piezoceramics. Four strategies of a potential importance were suggested and discussed to help researchers plan and design their future research on lead-free piezoceramics with a recently reported exemplary work.
Key words: Electrostrictions, Lead-free piezoceramics, Incipient piezoceramics, Reactive templated grain growth, Electromechanical strains
1. Introduction
Piezoelectricity is one of the representative functional properties where the crystallographic anisotropy plays the most important role. It follows that typical piezoelectric materials had been single crystals, exemplarily quartz, until the ferroelectric barium titanate (BaTiO 3, BT) was discovered during World War II. 1) This discovery of ferroelectricity, which enabled one to induce piezoelectricity even out of randomly-oriented ceramics, marked a historic moment, prospecting a ubiquitous utilization of piezoceramics that are cheaper with excellent functional properties. Indeed, the subsequent discovery of lead zirconate titanate (PZT) solid solution has led to an explosive growth of real world piezoelectric market with a special emphasis on actuators. 2,3) There is no doubt that the piezoelectric industry based on PZT has proven itself to be a great success with a number of practical applications from micro-scales to centimeter-scales, still expanding steadily with the introduction of new applications. Albeit the long-term success, the piezoceramic community has faced a new challenge imposed by worldwide environmental regulations, i.e., the removal of the ‘magic’ element, lead, out of piezoelements since early 2000s. Initially, the task appeared to be simple in that once an element that could replace the lead was discovered, the mission could be completed. However, it was not that easy as expected. As grasped from a number of review papers dedicated to the issue, 2-14) a considerable amount of time and resources have been devoted to the task intensively over the last decade, achieving only a handful of meaningful results. The aforementioned rather unsatisfactory outcome over the last decade was not hard for many researchers to foresee, considering the lack of decisive strategies apart from searching for the so-called morphotropic phase boundary (MPB), although the presence of MPB is not yet confirmed to be the necessary and sufficient condition for maximizing the properties of piezoceramics. 3) There is no doubt that the presence of MPB was one of the most important keys to the success of PZTs. The impact of the discovery of PZT was so great that most studies even for lead-free piezoceramics have been devoted blindly to a trial-and-error type of compositional searching for MPBs by mixing lead-free compounds of different symmetries, without paying a critical attention to what we could achieve at the end. As a part of the consequence, not much attention was paid to other potentially effective strategies that could further enhance the properties of piezoceramics, either. At this point, we believe that before we further make towards, it would be highly helpful if the accumulated data are critically reviewed to better understand where we are, to which direction we should move, what we can expect ultimately. In this regard, we have attempted to analyze the existing data both on PZTs and lead-free’s in a way that they could reveal some meaningful clues to the aforementioned queries. To show how effective the application of out-of-MPB type of approach could be, we present a way to make recently discovered incipient piezoelectric strains practical through a polarization-engineering strategy. 15)
2. State of the Art
2.1. Phase Instability vs. Piezoelectric Properties
The discovery of BT was, indeed, a historical turning point in the development of piezoceramics. Although MPB is the most famous keyword in the field of piezoceramics due to PZTs, the underlying principle, i.e., a property enhancement due to a phase instability, was already introduced during the study of BT. BT undergoes a series of phase transformations from rhombohedral to orthorhombic (or monoclinic a) and then to tetragonal with the increase in temperature, as illustrated in Fig. 1(a). 17) At each phase transformation temperature, physical properties such as dielectric permittivity ( ɛij), elastic compliance ( sij) and electromechanical coupling factor (
kij2) increase discontinuously. These changes in the physical properties leads to a discontinuous increase in d33 as well with the following fundamental equation: 3)
Here, the superscript T and E refer to a constant stress and electric field condition, respectively. The fact that piezoelectric properties peak at the temperature for each ferroelastic phase transformation b implies that for the same class of material systems, one could expect virtually enhanced piezoelectric properties when a nearby ferroelastic transformation temperature gets closer. On the other hand, it is well-known that the virtual enhancement of piezoelectric properties during a ferroelastic phase transformation is accompanied by a certain degree of an irreversible degradation in the properties. This is already self-explanatory by the peak in the properties, i.e., the properties culminate at the transformation temperature. As exemplarily shown in the Fig. 1(b), each thermal cycling through the orthorhombic to tetragonal transformation temperature ( TO-T) in a potassium sodium niobate (KNN) system deprives piezoelectric properties to a degree. Taking the aforementioned arguments into consideration, one may reach a conclusion that the possible upper operation temperature limit should be confined to the nearest ferroelastic phase transformation temperature, e.g., TO-T in KNN based systems, when TO-T is above room temperature. As well, the study of mechanism for any enhancement in piezoelectric properties of a certain system should consider the location of such ferroelastic phase transformation temperature. In the following discussion, we present analyzed data reinterpreted in accordance with these considerations.
2.2. Revisit to Lead-Based Piezoelectrics
In spite of the versatility of the PZT-based piezoceramics, there always has been a consistent demand on alternative piezoelectric materials with better performances. It means that any substitute should at least be competitive to PZTs in terms of functional properties. Then, a natural procedure to follow is to identify the status of the properties of PZTs as a guideline.
Figure 2(a) presents the piezoelectric charge (or strain) coefficient ( d33) of representative lead-based piezoceramics from the literature as a function of a reduced temperature c. As discussed in the previous section, the values reported in the literature can be reasonably compared, when their piezoelectric properties are plotted as a function of reduced temperature, which is defined as the temperature normalized by their depolarization temperature, i.e., Curie point here. It is interesting to see that though the data points are rather scattered, one can clearly notice that the d33 of lead-based piezoceramics 5,18) has a linear dependence on the reduced temperature. In other words, there is a trade-off between d33 in the Pb-based piezoceramics and the Curie point. Of course, this is not surprising in that d33, in general, tends to increase in approaching Tc, as long as there is no ferroelastic phase transformation in-between, 19) as discussed earlier. Nevertheless, an important conclusion to be drawn is that there exists a definite upper boundary for the attainable d33 in Pb-based piezoceramics, roughly at ~1100 pC/N, when one could somehow produce a PZT with its Curie point near room temperature. Here, an important thing to be noted is that d33 can be enhanced only at the expense of the reduction in Tc, which bounds the upper limit for operational temperature. Given that post-processing, exemplarily gluing typically practiced at an elevated temperature, or an enforced temperature range for operation for practical uses requires a range of temperature for stable functionality, the practically obtainable d33 is usually limited, as indicated by shaded region in Fig. 2(a).
Few would deny the fact that Pb is an indispensable element for perovskite-structured piezoceramics to deliver incomparably excellent properties and among all the best piezoceramics is PZT. 20) One of the best solutions to add up further desirable properties to PZT would be to make it a single crystalline form. As clearly illustrated in the classic textbook by Jaffe et al., 17) 100% domain alignment, which is the case for single crystals, is impossible in polycrystalline ceramics, since the allowed polarization directions in ferroelectric states are crystallographically restricted. For example, in the case of BT, only about 12% of ferroelastic (non-180°) domains could be aligned only closer to the field direction during poling process, though all ferroelectric (180°) domains are assumed to reach the closest possible alignment to the field direction. Even in the case of soft PZTs, where ferroelastic domains switch rather easier, the best alignment accomplished is less than 50%. 21,22) Then, one would say that the best scenario would be to grow single crystalline PZT. This is true, but it is unfortunate that PZT at the so-called morphotropic phase boundary (MPB), which is the most interesting composition with respect both to theory and to practice, cannot be grown into a single crystalline phase by conventional fabrication techniques due to its incongruent melting characteristics. 23-25)
Instead, various attempts to produce Pb-based single crystals have already been started in early 1960s with the socalled relaxor ferroelectric Pb(Mg 1/3Nb 2/3)O 3 (PMN). 26) A breakthrough was made when Park and Shrout 18) introduced PMN-PbTiO 3 (PMN-PT) and Pb(Zn 1/3Nb 2/3)O 3-PT (PZN-PT) single crystals, featured by extremely large small-and large-signal piezoelectric properties in spite of some controversial issues such as a new understanding of MPB. 3,27-31) Relaxor-PT-based single crystals indeed demonstrated the hypothesis that a single crystal is one of the most effective ways to overcome the upper limit for the piezoelectric properties potentially realizable by piezoceramics, as shown in Fig. 2(b). The piezoelectric business based on single crystals has successfully established its own market for high-end applications in transducers. 32,33)
2.3. Lead-Free Piezoelectrics: Status and Strategies
A big challenge has been taken by the piezoelectric community with the advent of environmental regulations, forcing lead to be removed from piezoelements. 3,5,7-9,11,13,14) Largely, two material systems have been considered to be of a potential interest as a consequence of extensive compositional searches over the last decade, i.e., (K 1-xNa x)NbO 3 (KNN) and its derivatives 13) and (Bi 1/2Na 1/2)TiO 3 (BNT)-based solid solutions. 3) Though these two systems are fundamentally different, the former is a normal ferroelectric, while the other an non-ergodic relaxor, their d33 values are well-aligned on a single line when plotted against a reduced temperature, leaving a potentially achievable maximum d33 at ~400 pC/N. Fig. 3 summarizes the state of the art of lead-free piezoceramics in terms of their d33 in comparison to PZT. Here, the reference temperature for KNN-based and BNT-based in calculating the reduced temperature was taken at TO-T and the temperature for induced ferroelectric to relaxor transition ( TF-R or commonly called Td), 2,34,35) respectively. A comparison with the line derived from PZT data reveals the reason why the search for lead-free piezoceramics alternative to PZTs based on the simple MPB-based approach have been largely unfruitful. The d33 values of each system both at a transition temperature, i.e., TR = 1, and in the window for practical uses are by far less than those of PZTs. It is obvious that no known lead-free piezoceramic could safely beat PZTs off for practical applications; thus, a special strategy should be applied. Single crystal approach 36-38) and texture-induced grain orientation approach 15,39-43) can be two readily available among such approaches. It is rather unfortunate to see that the data from the single crystals are too scattered for us to draw any decisive conclusion on the approach, leaving much room for potential improvements in their processing and properties. 37,44-53) The situation is not much different in the texture-induced grain orientation approach. As evident from Fig. 3, LF4T that triggered lead-free piezoelectric research worldwide was, indeed, a breakthrough, casting a hope that lead-free piezoceramics could replace PZTs with the aid of a grain orientation technique. 4,40) However, the effectiveness of the grain orientation technique has not been conclusively confirmed in other systems except for several reports on BT-based ceramics, yet. 54-58)
On the other hand, a recent report on Ba(Zr 0.2Ti 0.8)O 3- x(Ba 0.7Ca 0.3)TiO 3, 59) so-called BZT-BCT system, has drawn a considerable attention with its overwhelming piezoelectric properties in comparison to two representative lead-free systems such as BNT-based and KNN-based. The d33 value itself is the best among all the reported values in lead-free piezoceramics except for that of a couple of single crystals. It is interesting to see that BZT-BCT belongs neither to typical lead-free piezoceramic series nor to PZTs with a view to d33, though its applicability for practical uses is questionable. Attention needs paying to a recent report on BiFeO 3 (BF)-BT-based piezoceramics, prepared in a rather unusual way, i.e., relatively low-temperature sintering followed by a water quenching. 60) A series of compositions reported lie well on the PZT-line as well as within the typical processing window, proving their potential as commercializable piezoceramics in replace for PZTs. A concern could be their mechanical reliability due to thermal shock during water quenching procedure.
2.4. Incipient Piezostrains: A Newly Identified Strategy
2.4.1. Retrospective Summary of Incipient Piezostrains
As discussed in our previous review, 2) electric-field-induced strains in piezoceramics, i.e., polycrystalline ferroelectrics, can be classified into three distinct types. They can be discerned most clearly from their bipolar strain hysteresis.
a parabolic shape with negligible hysteresis, defined as an electrostrictive strain a butterfly shape with a square-type polarization hysteresis, defined as a piezoelectric strain a sprout shape with a double (or constricted) polarization hysteresis, defined as an incipient piezoelectric strain.
Among them, the incipient piezostrains are of a great interest. In general, they can reach at least two times larger than the other two due to the absence of the remanent strain typically inevitable to ferroelectrics. 61)
The first report on an incipient piezostrain was made on a BNT-BT single crystal near its alleged MPB composition in 1998. 62) At that time, the origin of the large incipient piezostrain was considered to originate from an electric-field-induced antiferroelectric-to-ferroelectric phase transformation, in reference to the earlier publication on the system. 63) This misinterpretation was again succeeded when the incipient strains were discovered in KNN-modified BNT-BT ceramics in 2007. 64-67) Later, it was experimentally demonstrated that the large incipient strain comes from an electricfield-induced reversible phase transformation between a ‘metrically’ d cubic and a ferroelectrically-active non-cubic phase. 61,68-71) The origin of the metrically cubic phase was identified when the base system, BNT-BT near the alleged MPB, is not a normal ferroelectric but a relaxor. 34,35,72)
Figure 4 illustrates schematically how the reported large strain is realized within the context of relaxor-based incipient piezoceramics. As noted, polarization ( P) and electric field ( E) are correlated by the following equation: 73,74)
where α, β, and γ are coefficients. The corresponding electric-field-induced strain (S) is expressed as
where Q denotes electrostrictive coefficient.
When an applied electric field is small, P and E are linearly proportional in the form of P = PS + ɛɛ0E, where PS, ɛ, and ɛ0 refer to spontaneous polarization that is negligible in paraelectrics, dielectric permittivity, and the vacuum permittivity, respectively. Given that ergodic relaxors are macroscopically paraelectric, PS is zero. Then, P linearly increases with increasing E as in Fig. 4(a). With further increasing E, P starts to saturate, resulting in S-shaped P- E curve ( Fig. 4(b)). However, when the electric field goes beyond a certain level, a long-range order begins to be established and reorient along the field direction, leading to a sudden increase both in P and S ( Fig. 4(c)). It is reasonable to think that the larger the PS inherent to the given material, the higher the P and S. Since the mechanism for the incipient piezostrains was understood based on their relaxor-based argument, attempts to utilize this large strain have been actively made targeting actuator applications. 2,3,75) The early stage of this study heavily focused on finding new compositions with as high strain level as possible. 76-97) Those extensive studies had identified largely three challenges to be overcome to make the incipient piezostrain practical.
The magnitude of electric field triggering such large incipient strains is too large from the practical point of view. The incipient strains are accompanied by a considerably large strain hysteresis. The achievable strain levels are highly dependent on the driving frequencies and operation temperatures.
The successive stage of the study has, of course, been dedicated to overcome the aforementioned challenges.
Given that the required large electric field and the frequency dependence of the incipient strains are closely related to the reversible phase transformation kinetics, Lee et al.98,99) embedded ferroelectric seed crystals to the incipient piezoceramics for them to facilitate the transformation kinetics. This idea turned out to be a reasonable success, supported by theoretical explanations. 75,100, 101) The first theoretical model regarded this 0 - 3 type composite as a serially connected capacitors so that the two phases are coupled in terms of polarization. 82) This model appeared to be good enough to clarify the 0 - 3 composite effect. However, a further experimental work 83) followed by a theoretical reasoning 57) revealed that in addition to the polarization coupling, a strain coupling, mechanically constraining each other due to the difference in the electrostrictive coefficient, also plays a significant role. So far, approaches by both core-shell composed of ferroelectric core and relaxor shell 89,97) and ferroelectric seed and relaxor shell have been proven quite successful, although a complete solution to the aforementioned three challenges seems inherently unachievable.
2.4.2. An Exemplary Work Providing Incipient Piezoceramics with a Future Direction
As discussed so far, the currently available techniques do not seem to resolve three challenges the relaxor-based incipient piezostrains are facing, requiring ingenious ideas. Recently, we proposed a way to potentially overcome all the addressed issues, using a lead-free ergodic relaxor BNT-(Bi 1/2K 1/2)TiO 3-BiAlO 3 (BNKT-BA) system. 15) Ironic as it may sound, it was shown that suppressing piezoelectric contribution could enhance the incipient strain properties significantly through a maximized contribution of electrostriction. As is well-known, the electrostrictive strain is as fast as the underlying polarization mechanism; thus, the frequency dependence and hysteresis caused during depolarization process during decreasing electric field could be largely overcome. As well, thanks to the temperature-insensitive electrostrictive coefficient, the temperature dependence of electrostrictive strains is also expected to be stable. Maximizing the electrostrictive effect by constraining polarization switching was realized by a so-called reactive templated grain growth (RTGG), 42) which is, of course, not a novel technique any more. As noted, the RTGG process has been widely utilized by the piezoelectric community for ceramics to mimic single crystals by aligning the spontaneous polarization axis of individual grains along the direction where external electric field is supposed to be applied. What makes it special in our study was to utilize the technique in an unusual way. Instead of following the conventional approach, we intentionally confined the spontaneous polarization axis in plane perpendicular to the electric-field direction. This was done by a partial converting of Na 0.5Bi 4.5Ti 4O 15 (NBiT) templates, the polarization direction of which is either a or b axis. 102, 103) Since the spontaneous polarization in NBiT templates develops along a or b axis passing through 658°C 102- 104) during cooling, this spontaneous polarization would be high enough to polarize the surrounding matrix BNKT-BA phase epitaxially at such a high temperature. In fact, the microstructure, presented in Fig. 5, confirms the expectation by the ubiquitous ferroelectric domain contrast, though the presented BNKT-BA composition is an ergodic relaxor state. 84)
The results of significance are summarized in Fig. 6. The X-ray diffraction profile of the as-textured clearly visualize the typical polarization axis of tetragonal phase, <002>, can hardly be traced along the direction where an external electric field is designed to be applied. As well, the appended electric-field-dependent in situ X-ray diffraction study confirms our expectation that the polarization switching should be strongly hindered, while a significant electrostriction should take place. The former is implied by the practically immobile (002) peak during the entire experiment, and the latter by the significantly decreasing position of (200) peak with increasing electric field intensity. These changes in the microstructure are well-manifested in the macroscopic strain property as shown in Fig. 6(b). As schematically illustrated in Fig. 6(c), the enhanced but a less hysteric strain behavior could be explained as follows:
The electrostrictive deformation becomes facilitated in the absence of piezoelectric contribution.105) The polarization vector constrained in-plane direction resists the in-plane shrinkage forced by Poisson’s ratio, which leads to the development of a compressive stress to the in-plane polarization. The compressive stress creates a piezoelectric effect negatively along the polarization direction, giving rise to a positive d31 effect along the field direction, reinforcing the magnitude of strain.
Consequently, the overall characteristics of the obtained strain follows those of electrostrictive strain, which is temperature- and frequency-insensitive and less hysteric.
3. Concluding Remarks
Taking d33 as a representative parameter in evaluating piezoproperties, the accumulated literature data both from lead-based and from lead-free piezoelectrics were reanalyzed. The analysis on PZT-based piezoceramics revealed a linear dependence of d33 on the measurement temperature normalized by each Curie point, indicating that the best achievable d33 in PZT-based piezoceramics could be around 1100 pC/N. The same analysis made on lead-free piezoceramics also resulted in a linear correlation between d33 and the measurement temperature normalized by the nearest depolarization temperature, leaving the maximum achievable d33 no more than 400 pC/N. We considered four strategies that could enable one to overcome the predicted limit, namely, single crystal approach, quenching-induced instability approach, grain-orientation approach, and incipient piezostrain approach. A successful example best-utilizing such techniques was presented and the underlying principle therein was discussed.
Acknowledgments
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MISP) (No. 2014R1A2A1A11053597). CWA acknowledges the financial supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2015R1D1A3A01019470).
Notes
In general, orthorhombic and monoclinic symmetries are clearly discerned. However, when the distortion is so small that crystallographic a and c axis are ‘metrically’ equivalent, orthorhombic unit cell with a doubled a and b edges is reduced to a monoclinic pseudo-cell, as pointed out by Megaw.16)
Notes
We intentionally used the term, the ferroelastic phase transformation, which is often referred to as a polymorphic phase transformation elsewhere, because even transformations such as non-ferroelectric centrosymmetric tetragonal to a cubic transformation are classified as polymorphic phase transformation, which we would like to exclude.
Notes
The d33 values in the literature are measured at room temperature, as long as the temperature is not specifically stated. Though room temperature varies from place to place, we took 298 K as room temperature en bloc for the sake of convenience. The reduced temperature was then defined as 298/Tc.
Notes
The word ‘metrically’ refers to the crystallographic structure determined by X-ray diffraction techniques.
Notes
Conflict of Interest
The authors declare no conflicts of interest.
Fig. 1
(a) Changes in parameters constituting d33 in the temperature range encompassing two ferroelastic transformations of BaTiO 3. 17) A discontinuous change signifies the effect of phase instability, which leads to an enhancement of d33. (b) The effect of the presence of a ferroelastic phase transition on the piezoelectricity-related properties of a KNN-LS piezoceramic. 106) Though the presence of such ferroelastic phase transition enhances the properties, it limits the maximum operation temperature, which is clear from a gradual degradation of the properties with thermal cyclings above the transition temperature. 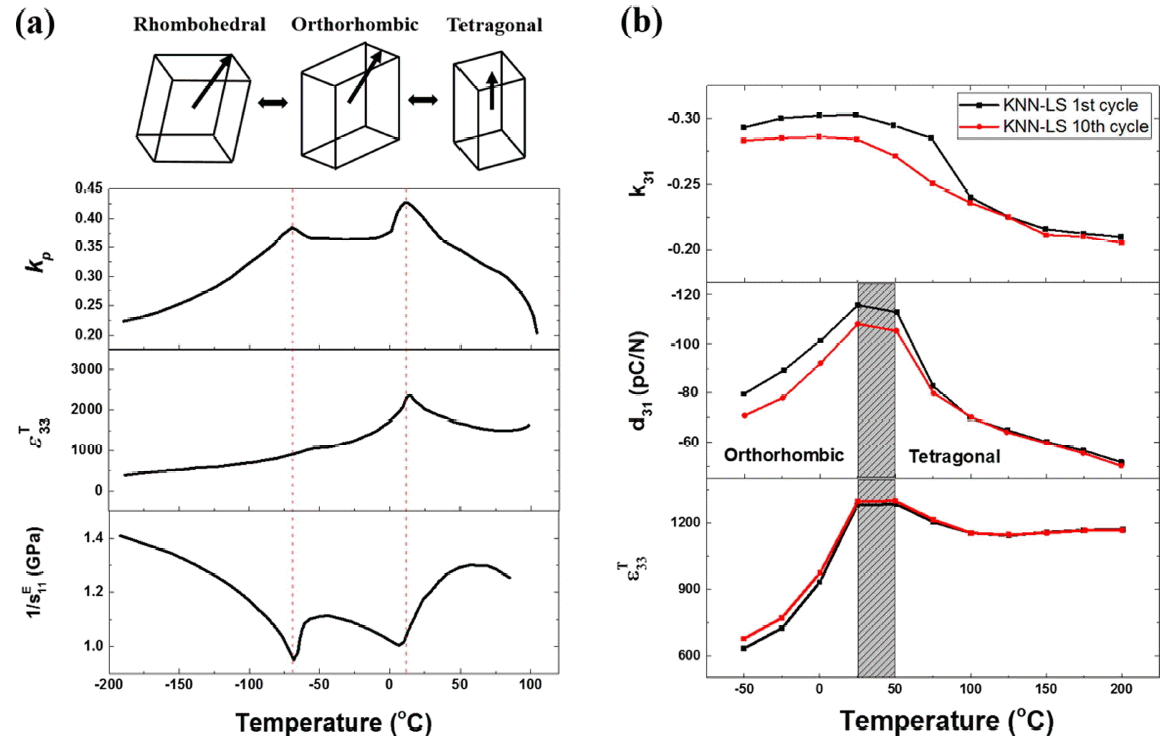
Fig. 2
(a) Literature data on d33 of PZTs and relaxor-PT ceramics plotted as a function of a reduced temperature. The window for practical uses is set based on long-term thermal stability. 5) (b) PZT-based data reinforced with single crystal data that justifies why single crystal approach is, in general, highly effective. 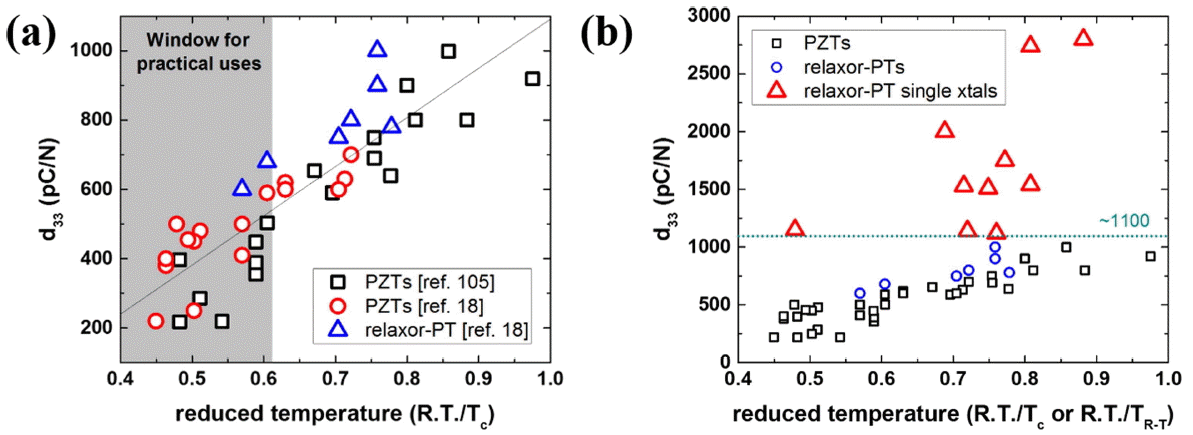
Fig. 3
The state of the art of d33 in lead-free piezoelectrics plotted with respect to reduced temperature. It is interesting to see that two representative lead-free piezoceramic systems, i.e., BNT-based and KNN-based, share the same single line in the plot, confirming the usefulness of reduced temperature as an evaluation parameter. It is noted that LF4 40) and quenched BF-BT-based piezoceramics 60) share the trend line with PZTs. 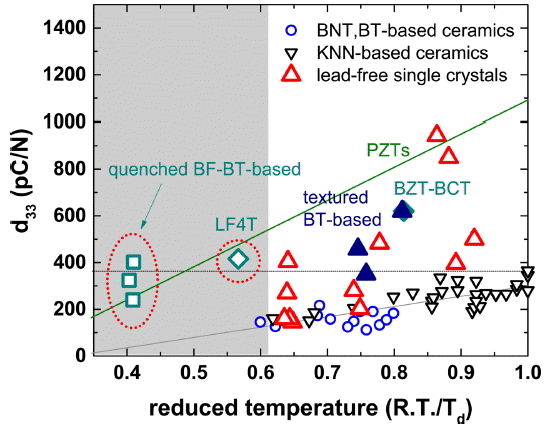
Fig. 4
Schematic illustration showing how incipient piezostrains develop in relaxor-based incipient piezoelectrics. Typically-denoted large (or giant) incipient piezostrains requires sufficiently large electric field to trigger the transformation from ergodic relaxor to ferroelectric as in (c). 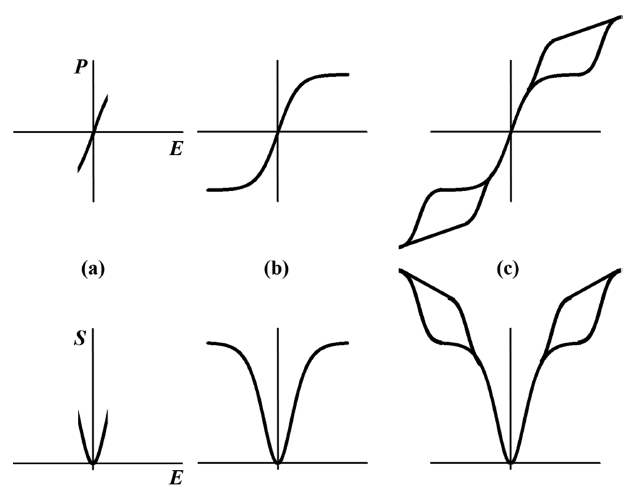
Fig. 5
A cross-sectional microstructure of grain-oriented BNKT-BA ceramic with its schematic representation. The cross-section was made perpendicular to the texture direction. 
Fig. 6
(a) In situ X-ray diffraction data on a selected 2-theta range covering (002) and (200) peaks as a function of electric field. It is clearly see that domain contribution is mostly suppressed within the resolution limit and significant change in (002) position is noted. (b) A comparison of unipolar strain between a conventional and a RTGG ceramic of the same composition. (c) One of the underlying mechanism for the significantly enhanced electrostrictive strain, even surpassing the strain achieved in the conventional piezoceramic where the relaxor-to-ferroelectric transformation is activated. 
REFERENCES
1. GH. Haertling, “Ferroelectric Ceramics: History and Technology,” J Am Ceram Soc, 82 [4] 797-818 (1999).  2. W. Jo, R. Dittmer, M. Acosta, J. Zang, C. Groh, E. Sapper, K. Wang, and J. Rödel, “Giant Electric-Field-Induced Strains in Lead-Free Piezoceramics for Actuator Applications - Status and Perspective,” J Electroceram, 29 [1] 71-93 (2012).  3. C-H. Hong, H-P. Kim, B-Y. Choi, H-S. Han, JS. Son, CW. Ahn, and W. Jo, “Lead-Free Piezoceramics - Where to Move On?,” J Materiomics, 2 [1] 1-24 (2016).  4. LE. Cross, “Materials Science: Lead-Free at Last,” Nature, 432 [7013] 24-25 (2004).  5. TR. Shrout, and SJ. Zhang, “Lead-Free Piezoelectric Ceramics: Alternatives for PZT?,” J Electroceram, 19 [1] 113-26 (2007).  6. T. Takenaka, H. Nagata, and Y. Hiruma, “Current Developments and Prospective of Lead-Free Piezoelectric Ceramics,” Jpn J Appl Phys, 47 [5] 3787-801 (2008).  7. PK. Panda, “Review: Environmental Friendly Lead-Free Piezoelectric Materials,” J Mater Sci, 44 [19] 5049-62 (2009).  8. J. Rödel, W. Jo, KTP. Seifert, E-M. Anton, T. Granzow, and D. Damjanovic, “Perspective on the Development of Lead-Free Piezoceramics,” J Am Ceram Soc, 92 [6] 1153-77 (2009).  9. D. Damjanovic, N. Klein, J. Li, and V. Porokhonskyy, “What Can Be Expected from Lead-Free Piezoelectric Materials?,” Funct Mater Lett, 3 [1] 5-13 (2010).  10. R-A. Eichel, and H. Kungl, “Recent Developments and Future Perspectives of Lead-Free Ferroelectrics,” Funct Mater Lett, 03 [01] 1-4 (2010).  11. E. Aksel, and JL. Jones, “Advances in Lead-Free Piezoelectric Materials for Sensors and Actuators,” Sensors (Basel), 10 [3] 1935-54 (2010).  12. I. Coondoo, N. Panwar, and A. Kholkin, “Lead-Free Piezoelectrics: Current Status and Perspectives,” J Adv Dielectrics, 3 [02] 1330002(2013).  13. J-F. Li, K. Wang, F-Y. Zhu, L-Q. Cheng, F-Z. Yao, and DJ. Green, “(K,Na)NbO3-Based Lead-Free Piezoceramics: Fundamental Aspects, Processing Technologies, and Remaining Challenges,” J Am Ceram Soc, 96 [12] 3677-96 (2013).  14. J. Rödel, KG. Webber, R. Dittmer, W. Jo, M. Kimura, and D. Damjanovic, “Transferring Lead-Free Piezoelectric Ceramics into Application,” J Eur Ceram Soc, 35 [6] 1659-81 (2015).  15. CW. Ahn, G. Choi, IW. Kim, J-S. Lee, K. Wang, Y. Hwang, and W. Jo, “Forced Electrostriction by Constraining Polarization Switching Enhances the Electromechanical Strain Properties of Incipient Piezoceramics,” NPG Asia Mater, 9 [1] e346(2017).  16. HD. Megaw, “Crystal Structure of Double Oxides of the Perovskite Type,” Proc Phys Soc, 58 [2] 133-52 (1946).  17. B. Jaffe, WR. Cook, and H. Jaffe, Piezoelectric Ceramics; pp. 16-83 Academic Press, London, 1971.
18. S-E. Park, and TR. Shrout, “Ultrahigh Strain and Piezoelectric Behavior in Relaxor Based Ferroelectric Single Crystals,” J Appl Phys, 82 [4] 1804-11 (1997).  19. T. Leist, J. Chen, W. Jo, E. Aulbach, J. Suffner, and J. Rödel, “Temperature Dependence of the Piezoelectric Coefficient in BiMeO3-PbTiO3 (Me=Fe, Sc, (Mg1/2Ti1/2)) Ceramics,” J Am Ceram Soc, 95 [2] 711-15 (2012).  20. RE. Cohen, “Origin of Ferroelectricity in Perovskite Oxides,” Nature, 358 [6382] 136-38 (1992).  21. JL. Jones, BJ. Iverson, and KJ. Bowman, “Texture and Anisotropy of Polycrystalline Piezoelectrics,” J Am Ceram Soc, 90 [8] 2297-314 (2007).  22. M. Deluca, “Microscopic Texture Characterisation in Piezoceramics,” Adv Appl Ceram, 115 [2] 112-22 (2016).  23. S. Fushimi, and T. Ikeda, “Phase Equilibrium in the System Pbo-TiO2-Zro2,” J Am Ceram Soc, 50 [3] 129-32 (1967).  24. T. Hatanaka, and H. Hasegawa, “Dielectric Properties of Pb(Zrxti1-x)O3 Single Crystals Including Monoclinic Zirconia,” Jpn J Appl Phys, Part 1, 34 [9B] 5446-48 (1995).  25. K-W. Kim, W. Jo, H-R. Jin, N-M. Hwang, and D-Y. Kim, “Abnormal Grain Growth of Lead Zirconium Titanate (PZT) Ceramics Induced by the Penetration Twin,” J Am Ceram Soc, 89 [5] 1530-33 (2006).  26. S. Zhang, and F. Li, “High Performance Ferroelectric Relaxor-PbTiO3 Single Crystals: Status and Perspective,” J Appl Phys, 111 [3] 031301(2012).  27. H. Fu, and RE. Cohen, “Polarization Rotation Mechanism for Ultrahigh Electromechanical Response in Single-Crystal Piezoelectrics,” Nature, 403 281-83 (2000).  28. B. Noheda, JA. Gonzalo, AC. Caballero, C. Moure, DE. Cox, and G. Shirane, “New Features of the Morphotropic Phase Boundary in the Pb(Zr1-xTix)O3 System,” Ferroelectrics, 237 [1] 237-44 (2000).  29. B. Noheda, JA. Gonzalo, R. Guo, S-E. Park, LE. Cross, DE. Cox, and G. Shirane, “The Monoclinic Phase in PZT: New Light on Morphotropic Phase Boundaries,” pp. 304-13 In: Fundamental Physics of Ferroelectrics 2000: Aspen Center for Physics Winter Workshop - Vol. 535 AIP Conference Proceedings; Aspen, Colorado, USA. 2000.  30. J. Frantti, Y. Fujioka, and RM. Nieminen, “Evidence against the Polarization Rotation Model of Piezoelectric Perovskites at the Morphotropic Phase Boundary,” J Phys: Condens Matter, 20 [47] 472203(2008).  31. AA. Heitmann, and GA. Rossetti, “Thermodynamics of Polar Anisotropy in Morphotropic Ferroelectric Solid Solutions,” Phil Mag, 90 [1-4] 71-87 (2010).  32. J. Chen, and R. Panda, “Review: Commercialization of Piezoelectric Single Crystals for Medical Imaging Applications,” pp. 235-240 In: IEEE Ultrasonics Symposium; Rotterdam, Netherlands. 2005.
33. E. Sun, and W. Cao, “Relaxor-Based Ferroelectric Single Crystals: Growth, Domain Engineering, Characterization and Applications,” Prog Mater Sci, 65 124-210 (2014).  34. W. Jo, and J. Rödel, “Electric-Field-Induced Volume Change and Room Temperature Phase Stability of (Bi1/2Na1/2)TiO3-x mol.% BaTiO3 Piezoceramics,” Appl Phys Lett, 99 [4] 042901(2011).  35. W. Jo, S. Schaab, E. Sapper, LA. Schmitt, H-J. Kleebe, AJ. Bell, and J. Rödel, “On the Phase Identity and Its Thermal Evolution of Lead-Free (Bi1/2Na1/2)TiO3 -6 mol% BaTiO3,” J Appl Phys, 110 [7] 074106(2011).  36. J-Y. Lee, H-T. Oh, and H-Y. Lee, ““Lead-Free” Piezoelectric Ba(Ti0.94Zr0.06)O3 single Crystals with Electromechanical Coupling Factor (K33) Higher Than 0.8,” J Korean Ceram Soc, 51 [6] 623-28 (2014).  37. J-Y. Lee, H-T. Oh, and H-Y. Lee, “Dielectric and Piezoelectric Properties of “Lead-Free” Piezoelectric Rhombohedral Ba(Ti0.92Zr0.08)O3 Single Crystals,” J Korean Ceram Soc, 53 [2] 171-77 (2016).   38. K-S. Moon, D. Rout, H-Y. Lee, and S-JL. Kang, “Solid State Growth of Na1/2Bi1/2TiO3-BaTiO3 Single Crystals and Their Enhanced Piezoelectric Properties,” J Cryst Growth, 317 [1] 28-31 (2011).  39. T. Kimura, T. Takahashi, T. Tani, and Y. Saito, “Crystallographic Texture Development in Bismuth Sodium Titanate Prepared by Reactive-Templated Grain Growth Method,” J Am Ceram Soc, 87 [8] 1424-29 (2004).  40. Y. Saito, H. Takao, T. Tani, T. Nonoyama, K. Takatori, T. Homma, T. Nagaya, and M. Nakamura, “Lead-Free Piezoceramics,” Nature, 432 [7013] 84-7 (2004).  41. Y. Seno, and T. Tani, “TEM Observation of a Reactive Template for Textured Bi0.5(Na0.87K0.13)0.5TiO3 Polycrystals,” Ferroelectrics, 224 [1] 365-72 (1999).  42. T. Tani, “Crystalline-Oriented Piezoelectric Bulk Ceramics with a Perovskite-Type Structure,” J Korean Phys Soc, 32 [93] S1217-S20 (1998).
43. CM. Fancher, W. Jo, J. Rödel, JE. Blendell, KJ. Bowman, and J. Ihlefeld, “Effect of Texture on Temperature-Dependent Properties of K0.5Na0.5NbO3 Modified Bi1/2Na1/2-TiO3-xBaTiO3,” J Am Ceram Soc, 97 [8] 2557-63 (2014).  44. K. Chen, G. Xu, D. Yang, X. Wang, and J. Li, “Dielectric and Piezoelectric Properties of Lead-Free 0.95(K0.5Na0.5)NbO3-0.05LiNbO3 Crystals Grown by the Bridgman Method,” J Appl Phys, 101 [4] 044103(2007).  45. H. Deng, X. Zhao, H. Zhang, C. Chen, X. Li, D. Lin, B. Ren, J. Jiao, and H. Luo, “Orientation Dependence of Electrical Properties of Large-Sized Sodium Potassium Niobate Lead-Free Single Crystals,” Cryst Eng Commun, 16 [13] 2760(2014).  46. W. Ge, H. Liu, X. Zhao, B. Fang, X. Li, F. Wang, D. Zhou, P. Yu, X. Pan, D. Lin, and H. Luo, “Crystal Growth and High Piezoelectric Performance of 0.95Na0.5Bi0.5TiO3-0.05BaTiO3 Lead-Free Ferroelectric Materials,” J Phys D: Appl Phys, 41 [11] 115403(2008).  47. J-Y. Lee, H-T. Oh, and H-Y. Lee, ““Lead-Free” Piezoelectric Ba(Ti0.94Zr0.06)O3 Single Crystals with Electromechanical Coupling Factor (K33) Higher Than 0.8,” J Korean Ceram Soc, 51 [6] 623-28 (2014).  48. D. Lin, Z. Li, S. Zhang, Z. Xu, and X. Yao, “Influence of MnO2 Doping on the Dielectric and Piezoelectric Properties and the Domain Structure in (K0.5Na0.5)NbO3 Single Crystals,” J Am Ceram Soc, 93 [4] 941-44 (2010).  49. G. Xu, Z. Duan, X. Wang, and D. Yang, “Growth and Some Electrical Properties of Lead-Free Piezoelectric Crystals (Na1/2Bi1/2)TiO3 and (Na1/2Bi1/2)TiO3-BaTiO3 Prepared by a Bridgman Method,” J Cryst Growth, 275 [1-2] 113-19 (2005).  50. X. Yi, H. Chen, W. Cao, M. Zhao, D. Yang, G. Ma, C. Yang, and J. Han, “Flux Growth and Characterization of Lead-Free Piezoelectric Single Crystal [Bi0.5(Na1-Xkx)0.5]TiO3,” J Cryst Growth, 281 [2-4] 364-69 (2005).  51. Z. Yu, R. Guo, and A. Bhalla, “Dielectric Polarization and Strain Behavior of Ba(Ti0.92 Zr0.08)O3 Single Crystals,” Mater Lett, 57 [2] 349-54 (2002).  52. Z. Yu, R. Guo, and AS. Bhalla, “Orientation Dependence of the Ferroelectric and Piezoelectric Behavior of Ba(Ti1-XZrx) O3 Single Crystals,” Appl Phys Lett, 77 [10] 1535-37 (2000).  53. Q. Zhang, Y. Zhang, F. Wang, Y. Wang, D. Lin, X. Zhao, H. Luo, W. Ge, and D. Viehland, “Enhanced Piezoelectric and Ferroelectric Properties in Mn-Doped Na0.5Bi0.5TiO3-BaTiO3 Single Crystals,” Appl Phys Lett, 95 [10] 102904(2009).  54. W. Bai, J. Hao, B. Shen, F. Fu, and J. Zhai, “Processing Optimization and Piezoelectric Properties of Textured Ba(Zr, Ti)O3 Ceramics,” J Alloys Compd, 536 189-97 (2012).  55. RE. Garcia, W. Craig Carter, and SA. Langer, “The Effect of Texture and Microstructure on the Macroscopic Properties of Polycrystalline Piezoelectrics: Application to Barium Titanate and PZN-PT,” J Am Ceram Soc, 88 [3] 750-57 (2005).  56. D. Liu, Y. Yan, and H. Zhou, “Synthesis of Micron-Scale Platelet BaTiO3,” J Am Ceram Soc, 90 [4] 1323-26 (2007).  57. T. Sato, Y. Yoshida, and T. Kimura, “Preparation of <110>-Textured BaTiO3 Ceramics by the Reactive-Templated Grain Growth Method Using Needlelike TiO2 Particles,” J Am Ceram Soc, 90 [9] 3005-8 (2007).  58. D. Vriami, D. Damjanovic, J. Vleugels, and O. Van der Biest, “Textured BaTiO3 by Templated Grain Growth and Electrophoretic Deposition,” J Mater Sci, 50 [24] 7896-907 (2015).  59. W. Liu, and X. Ren, “Large Piezoelectric Effect in Pb-Free Ceramics,” Phys Rev Lett, 103 [25] 257602(2009).  60. MH. Lee, DJ. Kim, JS. Park, SW. Kim, TK. Song, MH. Kim, WJ. Kim, D. Do, and IK. Jeong, “High-Performance Lead-Free Piezoceramics with High Curie Temperatures,” Adv Mater, 27 [43] 6976-82 (2015).  61. W. Jo, T. Granzow, E. Aulbach, J. Rödel, and D. Damjanovic, “Origin of the Large Strain Response in (K0.5Na0.5)NbO3-Modified (Bi0.5Na0.5)TiO3-BaTiO3 Lead-Free Piezoceramics,” J Appl Phys, 105 [9] 094102(2009).  62. YM. Chiang, GW. Farrey, and AN. Soukhojak, “Lead-Free High-Strain Single-Crystal Piezoelectrics in the Alkaline-Bismuth-Titanate Perovskite Family,” Appl Phys Lett, 73 [25] 3683-85 (1998).  63. T. Takenaka, K-I. Maruyama, and K. Sakata, “(Bi1/2Na1/2)TiO3-BaTiO3 System for Lead-Free Piezoelectric Ceramics,” Jpn J Appl Phys, 30 [9B] 2236-39 (1991).  64. S-T. Zhang, AB. Kounga, E. Aulbach, H. Ehrenberg, and J. Rödel, “Giant Strain in Lead-Free Piezoceramics Bi0.5Na0.5-TiO3-BaTiO3-K0.5Na0.5NbO3 System,” Appl Phys Lett, 91 [11] 112906(2007).  65. S-T. Zhang, AB. Kounga, E. Aulbach, T. Granzow, W. Jo, H-J. Kleebe, and J. Rödel, “Lead-Free Piezoceramics with Giant Strain in the System Bi0.5Na0.5TiO3-BaTiO3-K0.5Na0.5NbO3. I. Structure and Room Temperature Properties,” J Appl Phys, 103 [3] 034107(2008).  66. S-T. Zhang, AB. Kounga, E. Aulbach, W. Jo, T. Granzow, H. Ehrenberg, and J. Rödel, “Lead-Free Piezoceramics with Giant Strain in the System Bi0.5Na0.5TiO3-BaTiO3-K0.5Na0.5NbO3. II. Temperature Dependent Properties,” J Appl Phys, 103 [3] 034108(2008).  67. S-T. Zhang, AB. Kounga, W. Jo, C. Jamin, K. Seifert, T. Granzow, J. Rödel, and D. Damjanovic, “High-Strain Lead-Free Antiferroelectric Electrostrictors,” Adv Mater, 21 [46] 4716-20 (2009).  68. JE. Daniels, W. Jo, J. Rödel, V. Honkimäki, and JL. Jones, “Electric-Field-Induced Phase-Change Behavior in (Bi0.5Na0.5)TiO3-BaTiO3-(K0.5Na0.5)NbO3: A Combinatorial Investigation,” Acta Mater, 58 [6] 2103-11 (2010).  69. JE. Daniels, W. Jo, J. Rödel, and JL. Jones, “Electric-Field-Induced Phase Transformation at a Lead-Free Morphotropic Phase Boundary: Case Study in a 93%(Bi0.5Na0.5)-TiO3-7%BaTiO3 Piezoelectric Ceramics,” Appl Phys Lett, 95 [3] 032904(2009).  70. M. Hinterstein, M. Knapp, M. Hölzel, W. Jo, A. Cervellino, H. Ehrenberg, and H. Fuess, “Field-Induced Phase Transition in Bi1/2Na1/2TiO3-Based Lead-Free Piezoelectric Ceramics,” J Appl Cryst, 43 [6] 1314-21 (2010).   71. J. Kling, X. Tan, W. Jo, H-J. Kleebe, H. Fuess, and J. Rödel, “In Situ Transmission Electron Microscopy of Electric Field-Triggered Reversible Domain Formation in Bi-Based Lead Free Piezoceramics,” J Am Ceram Soc, 93 [9] 2452-55 (2010).  72. W. Jo, JE. Daniels, JL. Jones, X. Tan, PA. Thomas, D. Damjanovic, and J. Rödel, “Evolving Morphotropic Phase Boundary in Lead-Free (Bi1/2Na1/2)TiO3-BaTiO3 Piezoceramics,” J Appl Phys, 109 [1] 014110(2011).  73. AF. Devonshire, “Theory of Ferroelectrics,” Adv Phys, 3 [10] 85-130 (1954).  74. HF. Kay, “Electrostriction,” Rep Prog Phys, 18 [1] 230-50 (1955).  75. CW. Ahn, C-H. Hong, B-Y. Choi, H-P. Kim, H-S. Han, Y. Hwang, W. Jo, K. Wang, J-F. Li, J-S. Lee, and IW. Kim, “A Brief Review on Relaxor Ferroelectrics and Selected Issues in Lead-Free Relaxors,” J Korean Phys Soc, 68 [12] 1481-94 (2016).   76. Y. Hiruma, Y. Imai, Y. Watanabe, H. Nagata, and T. Takenaka, “Large Electrostrain near the Phase Transition Temperature of (Bi0.5Na0.5)TiO3-SrTiO3 Ferroelectric Ceramics,” Appl Phys Lett, 92 [26] 262904(2008).  77. Y. Hiruma, H. Nagata, and T. Takenaka, “Phase Diagrams and Electrical Properties of (Bi1/2Na1/2)TiO3-Based Solid Solutions,” J Appl Phys, 104 [12] 124106(2008).  78. R. Zuo, C. Ye, X. Fang, and J. Li, “Tantalum Doped 0.94Bi0.5Na0.5TiO3-0.06BaTiO3 Piezoelectric Ceramics,” J Eur Ceram Soc, 28 [4] 871-77 (2008).  79. Y. Hiruma, H. Nagata, and T. Takenaka, “Formation of Morphotropic Phase Boundary and Electrical Properties of (Bi1/2Na1/2)TiO3-Ba(Al1/2Nb1/2)O3 Solid Solution Ceramics,” Jpn J Appl Phys, 48 [9] 09KC08(2009).  80. Y. Hiruma, H. Nagata, and T. Takenaka, “Detection of Morphotropic Phase Boundary of (Bi1/2Na1/2)TiO3-Ba(Al1/2-Sb1/2)O3 Solid-Solution Ceramics,” Appl Phys Lett, 95 [5] 052903(2009).  81. KTP. Seifert, W. Jo, and J. Rödel, “Temperature-Insensitive Large Strain of (Bi1/2Na1/2)TiO3-(Bi1/2K1/2)TiO3-(K0.5Na0.5)-NbO3 Lead-Free Piezoceramics,” J Am Ceram Soc, 93 [5] 1392-96 (2010).
82. A. Hussain, CW. Ahn, JS. Lee, A. Ullah, and IW. Kim, “Large Electric-Field-Induced Strain in Zr-Modified Lead-Free Bi0.5(Na0.78K0.22)0.5TiO3 Piezoelectric Ceramics,” Sens Actuators, A, 158 [1] 84-89 (2010).  83. A. Hussain, CW. Ahn, A. Ullah, JS. Lee, and IW. Kim, “Effects of Hafnium Substitution on Dielectric and Electromechanical Properties of Lead-Free Bi0.5(Na0.78K0.22)0.5-(Ti1-xHfx)O3 Ceramics,” Jpn J Appl Phys, 49 [4] 041504(2010).  84. A. Ullah, CW. Ahn, A. Hussain, SY. Lee, HJ. Lee, and IW. Kim, “Phase Transitions and Large Electric Field-Induced Strain in BiAlO3-Modified Bi0.5(Na, K)0.5TiO3 Lead-Free Piezoelectric Ceramics,” Curr Appl Phys, 10 [4] 1174-81 (2010).  85. K-N. Pham, A. Hussain, CW. Ahn, W. Kim, SJ. Jeong, and J-S. Lee, “Giant Strain in Nb-Doped Bi0.5(Na0.82K0.18)0.5TiO3 Lead-Free Electromechanical Ceramics,” Mater Lett, 64 [20] 2219-22 (2010).  86. R. Dittmer, W. Jo, J. Daniels, S. Schaab, and J. Rödel, “Relaxor Characteristics of Morphotropic Phase Boundary (Bi1/2Na1/2)TiO3-(Bi1/2K1/2)TiO3 Modified with Bi(Zn1/2Ti1/2)O3,” J Am Ceram Soc, 94 [12] 4283-90 (2011).  87. W. Krauss, D. Schütz, M. Naderer, D. Orosel, and K. Reichmann, “BNT-Based Multilayer Device with Large and Temperature Independent Strain Made by a Water-Based Preparation Process,” J Eur Ceram Soc, 31 [9] 1857-60 (2011).  88. FF. Wang, M. Xu, YX. Tang, T. Wang, WZ. Shi, and CM. Leung, “Large Strain Response in the Ternary Bi0.5Na0.5-TiO3-BaTiO3-SrTiO3 Solid Solutions,” J Am Ceram Soc, 95 [6] 1955-59 (2012).  89. S-Y. Choi, S-J. Jeong, D-S. Lee, M-S. Kim, J-S. Lee, JH. Cho, BI. Kim, and Y. Ikuhara, “Gigantic Electrostrain in Duplex Structured Alkaline Niobates,” Chem Mater, 24 [17] 3363-69 (2012).  90. H-S. Han, W. Jo, J. Rödel, I-K. Hong, W-P. Tai, and J-S. Lee, “Coexistence of Ergodicity and Nonergodicity in LaFeO3-Modified Bi1/2(Na0.78K0.22)1/2TiO3 Relaxors,” J Phys: Condens Matter, 24 [36] 365901(2012).  91. V-Q. Nguyen, H-S. Han, K-J. Kim, D-D. Dang, K-K. Ahn, and J-S. Lee, “Strain Enhancement in Bi1/2(Na0.82K0.12)1/2TiO3 Lead-Free Electromechanical Ceramics by Co-Doping with Li and Ta,” J Alloy Compd, 511 [1] 237-41 (2012).  92. R. Dittmer, W. Jo, E. Aulbach, T. Granzow, and J. Roödel, “Frequency-Dependence of Large-Signal Properties in Lead-Free Piezoceramics,” J Appl Phys, 112 [1] 014101(2012).  93. H-S. Han, W. Jo, J-K. Kang, C-W. Ahn, I. Won Kim, K-K. Ahn, and J-S. Lee, “Incipient Piezoelectrics and Electrostriction Behavior in Sn-Doped Bi1/2(Na0.82K0.18)1/2TiO3 Lead-Free Ceramics,” J Appl Phys, 113 [15] 154102(2013).  94. HB. Lee, DJ. Heo, RA. Malik, CH. Yoon, H-S. Han, and JS. Lee, “Lead-Free Bi1/2(Na0.82K0.18)1/2TiO3 Ceramcis Exhibiting Large Strain with Small Hysteresis,” Ceram Int, 39 [S1] S705-8 (2013).  95. C. Groh, W. Jo, and J. Rödel, “Frequency and Temperature Dependence of Actuating Performance of Bi1/2Na1/2TiO3-BaTiO3 Based Relaxor/Ferroelectric Composites,” J Appl Phys, 115 [23] 234107(2014).  96. HS. Han, IK. Hong, Y-M. Kong, JS. Lee, and W. Jo, “Effect of Nb Doping on the Dielectric and Strain Properties of Lead-Free 0.94(Bi1/2Na1/2)TiO3-0.06BaTiO3 Ceramics,” J Korean Ceram Soc, 53 [2] 145-49 (2016).   97. M. Acosta, W. Jo, J. Rödel, and DC. Lupascu, “Temperature-and Frequency-Dependent Properties of the 0.75Bi1/2Na1/2TiO3-0.25SrTiO3 Lead-Free Incipient Piezoceramic,” J Am Ceram Soc, 97 [6] 1937-43 (2014).  98. DS. Lee, DH. Lim, MS. Kim, KH. Kim, and SJ. Jeong, “Electric Field-Induced Deformation Behavior in Mixed Bi0.5Na0.5TiO3 and Bi0.5(Na0.75K0.25)0.5TiO3-BiAlO3,” Appl Phys Lett, 99 [6] 062906(2011).  99. D-S. Lee, SJ. Jeong, MS. Kim, and JH. Koh, “Electric Field Induced Polarization and Strain of Bi-Based Ceramic Composites,” J Appl Phys, 112 [12] 124109(2012).  100. C. Groh, DJ. Franzbach, W. Jo, KG. Webber, J. Kling, LA. Schmitt, HJ. Kleebe, S-J. Jeong, J-S. Lee, and J. Rödel, “Relaxor/Ferroelectric Composites: A Solution in the Quest for Practically Viable Lead-Free Incipient Piezoceramics,” Adv Funct Mater, 24 [3] 356-62 (2013).  101. H. Zhang, C. Groh, Q. Zhang, W. Jo, KG. Webber, and J. Rödel, “Large Strain in Relaxor/Ferroelectric Composite Lead-Free Piezoceramics,” Adv Electron Mater, 1 [6] 1500018(2015).  102. T. Takenaka, K. Sakata, and K. Toda, “Piezoelectric Properties of Bismuth Layer-Structured Ferroelectric Na0. 5Bi4. 5-Ti4O15 Ceramic,” Jpn J Appl Phys, 24 [S2] 730(1985).  103. JS. Kim, CW. Ahn, DS. Lee, IW. Kim, JS. Lee, BM. Jin, and SH. Bae, “An Advanced Ferroelectric Properties of the Mn Doped Na0.5Bi4.5Ti4O15 Ceramics Fabricated by Hot-Forging Method,” Ferroelectrics, 332 [1] 45-9 (2006).  104. C-M. Wang, L. Zhao, J-F. Wang, S. Zhang, and TR. Shrout, “Enhanced Piezoelectric Properties of Sodium Bismuth Titanate (Na0.5Bi4.5Ti4O15) Ceramics with B-Site Cobalt Modification,” Phys Status Solidi, 3 [1] 7-9 (2009).
105. F. Li, L. Jin, Z. Xu, and S. Zhang, “Electrostrictive Effect in Ferroelectrics: An Alternative Approach to Improve Piezoelectricity,” Appl Phys Rev, 1 [1] 011103(2014).  106. S. Zhang, R. Xia, H. Hao, H. Liu, and TR. Shrout, “Mitigation of Thermal and Fatigue Behavior in K0.5Na0.5NbO3-Based Lead Free Piezoceramics,” Appl Phys Lett, 92 [15] 152904-43 (2008). 
|
|

















